Towards Sharper Risk Bounds for Minimax Problems
Paper and Code
Oct 11, 2024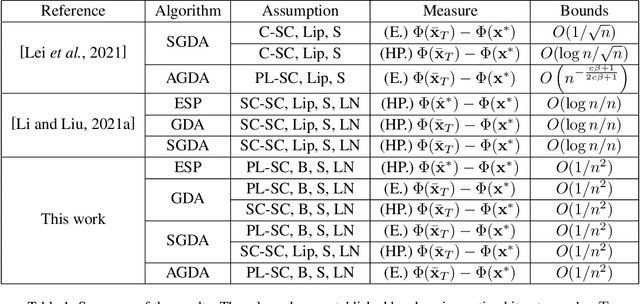
Minimax problems have achieved success in machine learning such as adversarial training, robust optimization, reinforcement learning. For theoretical analysis, current optimal excess risk bounds, which are composed by generalization error and optimization error, present 1/n-rates in strongly-convex-strongly-concave (SC-SC) settings. Existing studies mainly focus on minimax problems with specific algorithms for optimization error, with only a few studies on generalization performance, which limit better excess risk bounds. In this paper, we study the generalization bounds measured by the gradients of primal functions using uniform localized convergence. We obtain a sharper high probability generalization error bound for nonconvex-strongly-concave (NC-SC) stochastic minimax problems. Furthermore, we provide dimension-independent results under Polyak-Lojasiewicz condition for the outer layer. Based on our generalization error bound, we analyze some popular algorithms such as empirical saddle point (ESP), gradient descent ascent (GDA) and stochastic gradient descent ascent (SGDA). We derive better excess primal risk bounds with further reasonable assumptions, which, to the best of our knowledge, are n times faster than exist results in minimax problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge