Optimizing the optimizer for data driven deep neural networks and physics informed neural networks

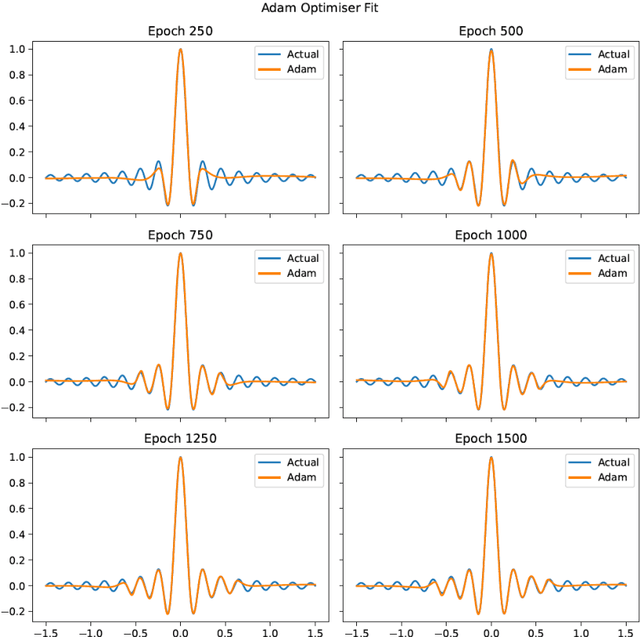
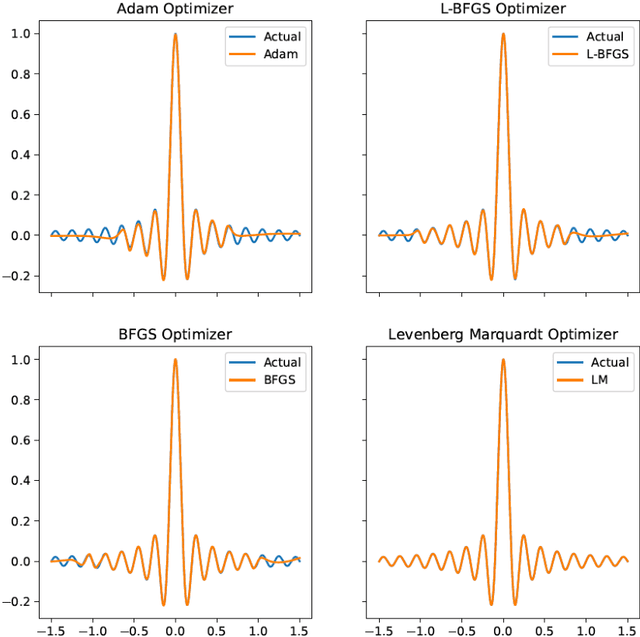
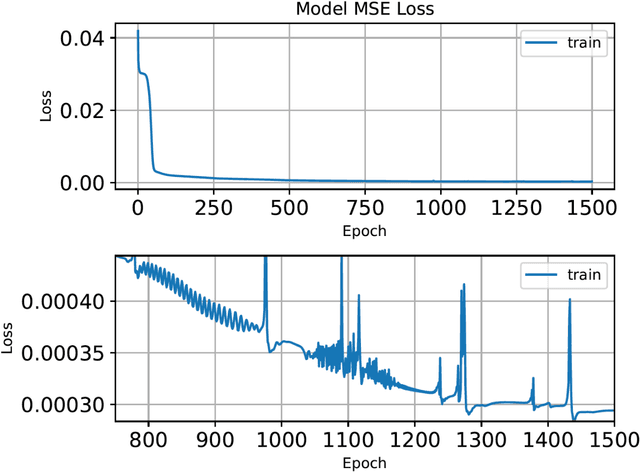
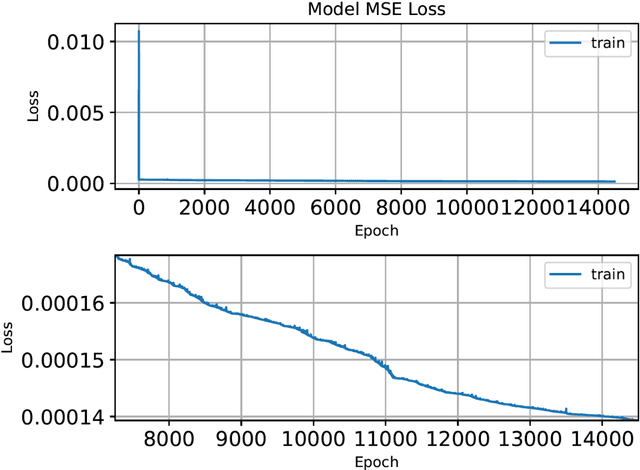
We investigate the role of the optimizer in determining the quality of the model fit for neural networks with a small to medium number of parameters. We study the performance of Adam, an algorithm for first-order gradient-based optimization that uses adaptive momentum, the Levenberg and Marquardt (LM) algorithm a second order method, Broyden,Fletcher,Goldfarb and Shanno algorithm (BFGS) a second order method and LBFGS, a low memory version of BFGS. Using these optimizers we fit the function y = sinc(10x) using a neural network with a few parameters. This function has a variable amplitude and a constant frequency. We observe that the higher amplitude components of the function are fitted first and the Adam, BFGS and LBFGS struggle to fit the lower amplitude components of the function. We also solve the Burgers equation using a physics informed neural network(PINN) with the BFGS and LM optimizers. For our example problems with a small to medium number of weights, we find that the LM algorithm is able to rapidly converge to machine precision offering significant benefits over other optimizers. We further investigated the Adam optimizer with a range of models and found that Adam optimiser requires much deeper models with large numbers of hidden units containing up to 26x more parameters, in order to achieve a model fit close that achieved by the LM optimizer. The LM optimizer results illustrate that it may be possible build models with far fewer parameters. We have implemented all our methods in Keras and TensorFlow 2.

Exploiting the Power of Levenberg-Marquardt Optimizer with Anomaly Detection in Time Series

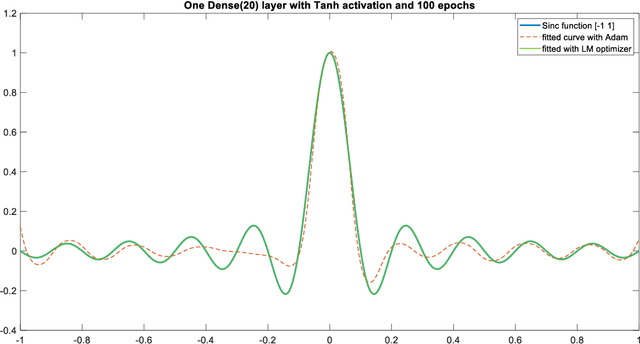
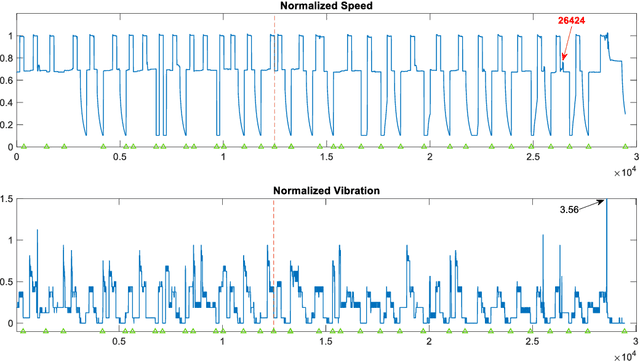
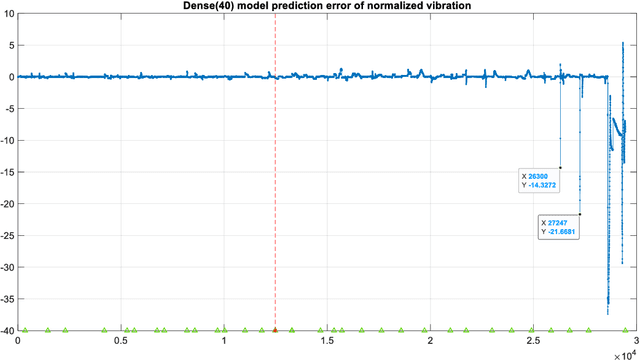
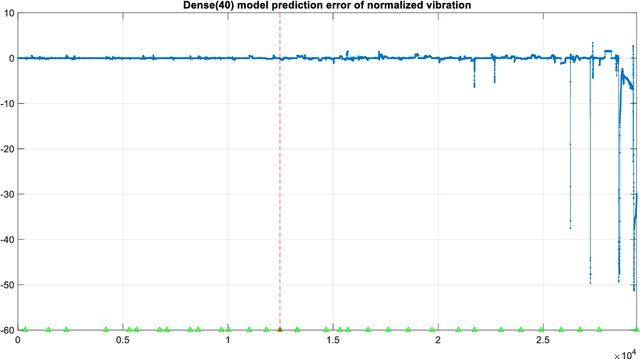
The Levenberg-Marquardt (LM) optimization algorithm has been widely used for solving machine learning problems. Literature reviews have shown that the LM can be very powerful and effective on moderate function approximation problems when the number of weights in the network is not more than a couple of hundred. In contrast, the LM does not seem to perform as well when dealing with pattern recognition or classification problems, and inefficient when networks become large (e.g. with more than 500 weights). In this paper, we exploit the true power of LM algorithm using some real world aircraft datasets. On these datasets most other commonly used optimizers are unable to detect the anomalies caused by the changing conditions of the aircraft engine. The challenging nature of the datasets are the abrupt changes in the time series data. We find that the LM optimizer has a much better ability to approximate abrupt changes and detect anomalies than other optimizers. We compare the performance, in addressing this anomaly/change detection problem, of the LM and several other optimizers. We assess the relative performance based on a range of measures including network complexity (i.e. number of weights), fitting accuracy, over fitting, training time, use of GPUs and memory requirement etc. We also discuss the issue of robust LM implementation in MATLAB and Tensorflow for promoting more popular usage of the LM algorithm and potential use of LM optimizer for large-scale problems.