Optimizing the optimizer for data driven deep neural networks and physics informed neural networks
Paper and Code
May 16, 2022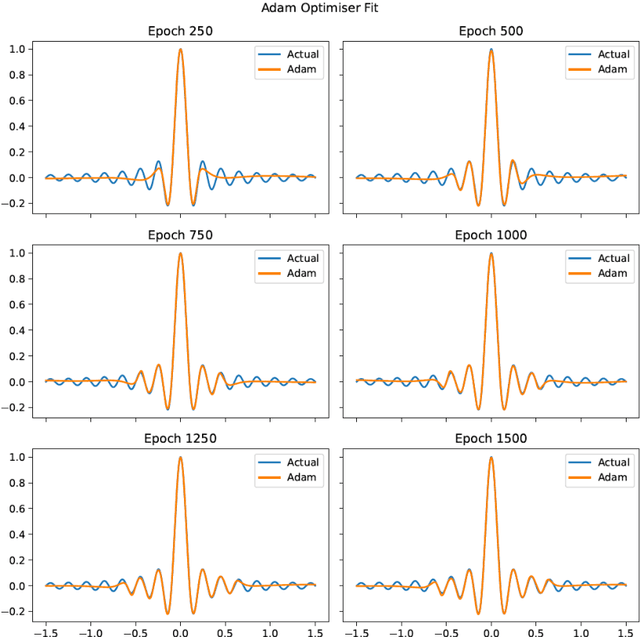
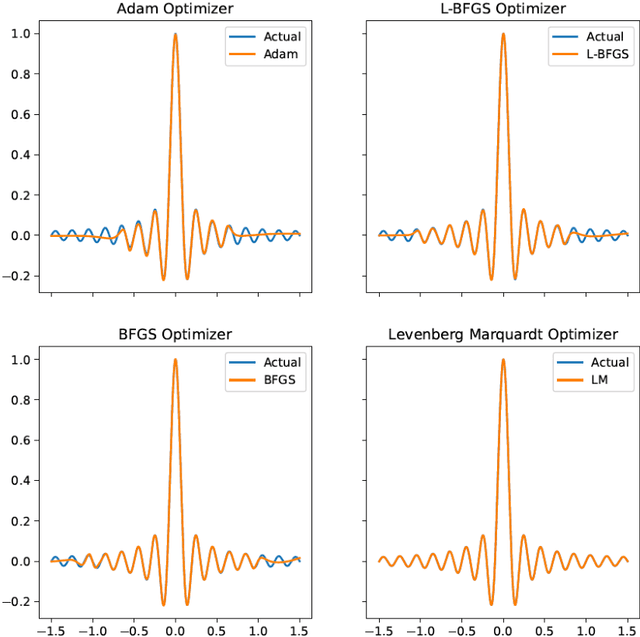
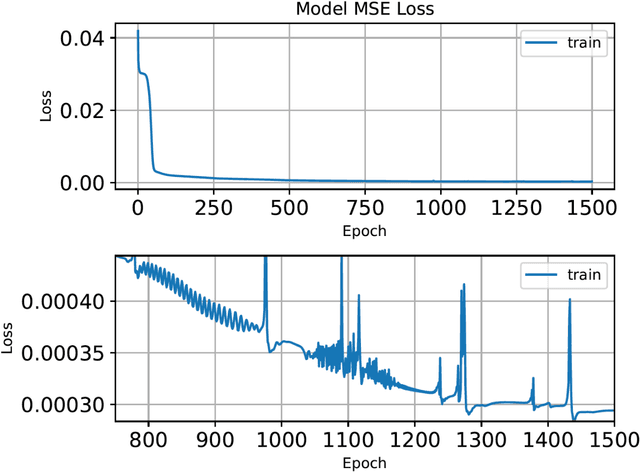
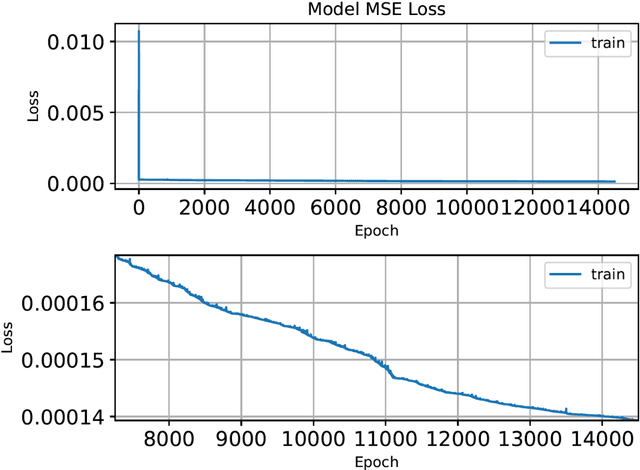
We investigate the role of the optimizer in determining the quality of the model fit for neural networks with a small to medium number of parameters. We study the performance of Adam, an algorithm for first-order gradient-based optimization that uses adaptive momentum, the Levenberg and Marquardt (LM) algorithm a second order method, Broyden,Fletcher,Goldfarb and Shanno algorithm (BFGS) a second order method and LBFGS, a low memory version of BFGS. Using these optimizers we fit the function y = sinc(10x) using a neural network with a few parameters. This function has a variable amplitude and a constant frequency. We observe that the higher amplitude components of the function are fitted first and the Adam, BFGS and LBFGS struggle to fit the lower amplitude components of the function. We also solve the Burgers equation using a physics informed neural network(PINN) with the BFGS and LM optimizers. For our example problems with a small to medium number of weights, we find that the LM algorithm is able to rapidly converge to machine precision offering significant benefits over other optimizers. We further investigated the Adam optimizer with a range of models and found that Adam optimiser requires much deeper models with large numbers of hidden units containing up to 26x more parameters, in order to achieve a model fit close that achieved by the LM optimizer. The LM optimizer results illustrate that it may be possible build models with far fewer parameters. We have implemented all our methods in Keras and TensorFlow 2.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge