Bijiao Wu
Kronecker CP Decomposition with Fast Multiplication for Compressing RNNs
Aug 21, 2020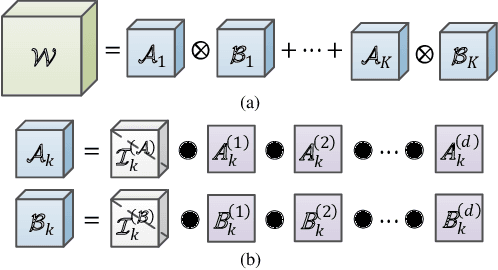
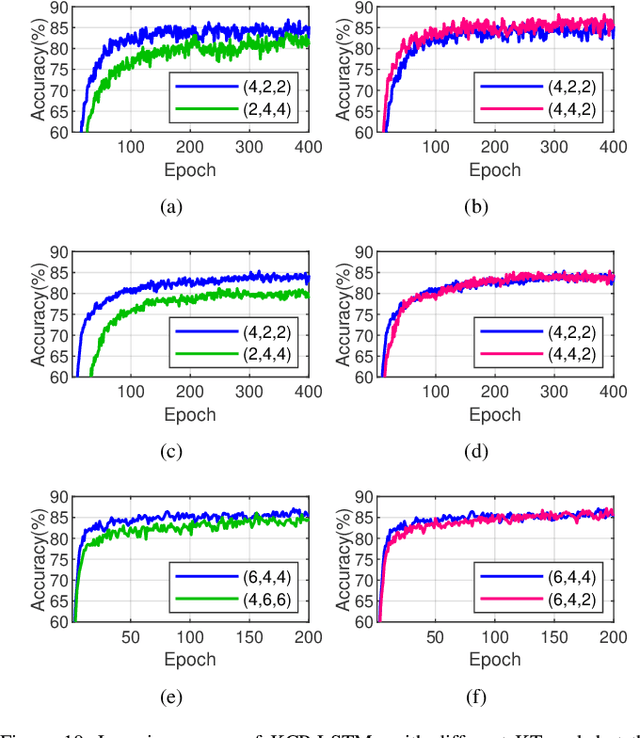
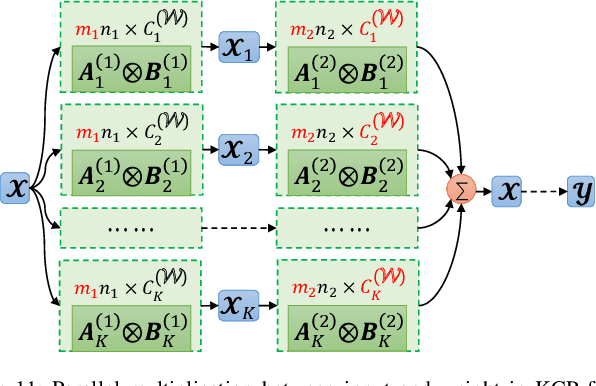
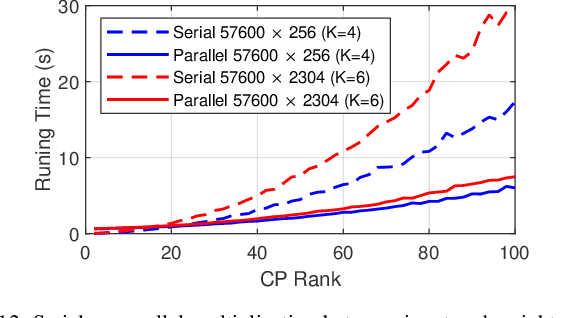
Abstract:Recurrent neural networks (RNNs) are powerful in the tasks oriented to sequential data, such as natural language processing and video recognition. However, since the modern RNNs, including long-short term memory (LSTM) and gated recurrent unit (GRU) networks, have complex topologies and expensive space/computation complexity, compressing them becomes a hot and promising topic in recent years. Among plenty of compression methods, tensor decomposition, e.g., tensor train (TT), block term (BT), tensor ring (TR) and hierarchical Tucker (HT), appears to be the most amazing approach since a very high compression ratio might be obtained. Nevertheless, none of these tensor decomposition formats can provide both the space and computation efficiency. In this paper, we consider to compress RNNs based on a novel Kronecker CANDECOMP/PARAFAC (KCP) decomposition, which is derived from Kronecker tensor (KT) decomposition, by proposing two fast algorithms of multiplication between the input and the tensor-decomposed weight. According to our experiments based on UCF11, Youtube Celebrities Face and UCF50 datasets, it can be verified that the proposed KCP-RNNs have comparable performance of accuracy with those in other tensor-decomposed formats, and even 278,219x compression ratio could be obtained by the low rank KCP. More importantly, KCP-RNNs are efficient in both space and computation complexity compared with other tensor-decomposed ones under similar ranks. Besides, we find KCP has the best potential for parallel computing to accelerate the calculations in neural networks.
Hybrid Tensor Decomposition in Neural Network Compression
Jun 29, 2020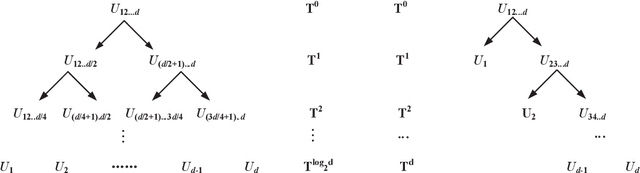
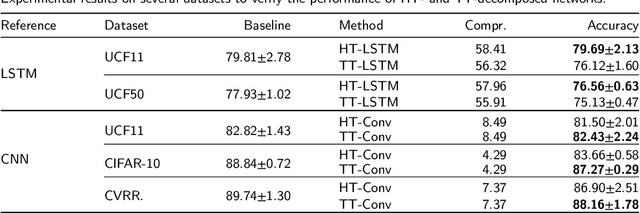
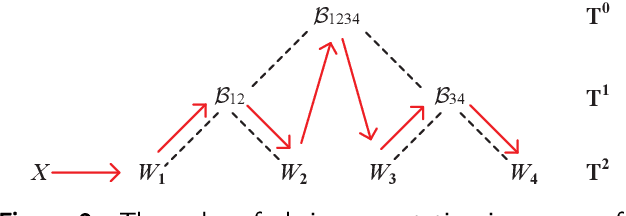
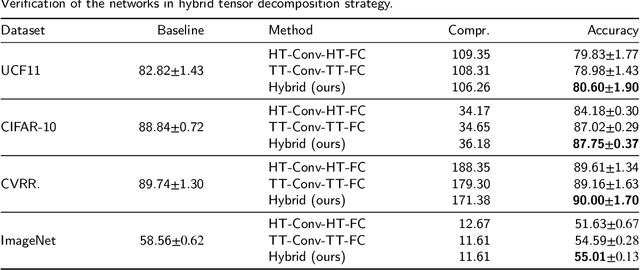
Abstract:Deep neural networks (DNNs) have enabled impressive breakthroughs in various artificial intelligence (AI) applications recently due to its capability of learning high-level features from big data. However, the current demand of DNNs for computational resources especially the storage consumption is growing due to that the increasing sizes of models are being required for more and more complicated applications. To address this problem, several tensor decomposition methods including tensor-train (TT) and tensor-ring (TR) have been applied to compress DNNs and shown considerable compression effectiveness. In this work, we introduce the hierarchical Tucker (HT), a classical but rarely-used tensor decomposition method, to investigate its capability in neural network compression. We convert the weight matrices and convolutional kernels to both HT and TT formats for comparative study, since the latter is the most widely used decomposition method and the variant of HT. We further theoretically and experimentally discover that the HT format has better performance on compressing weight matrices, while the TT format is more suited for compressing convolutional kernels. Based on this phenomenon we propose a strategy of hybrid tensor decomposition by combining TT and HT together to compress convolutional and fully connected parts separately and attain better accuracy than only using the TT or HT format on convolutional neural networks (CNNs). Our work illuminates the prospects of hybrid tensor decomposition for neural network compression.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge