Hybrid Tensor Decomposition in Neural Network Compression
Paper and Code
Jun 29, 2020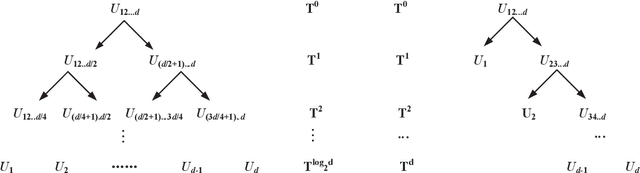
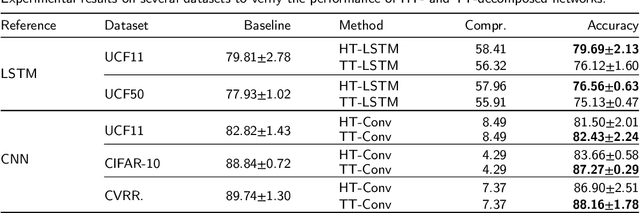
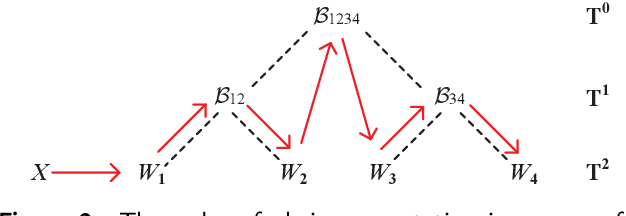
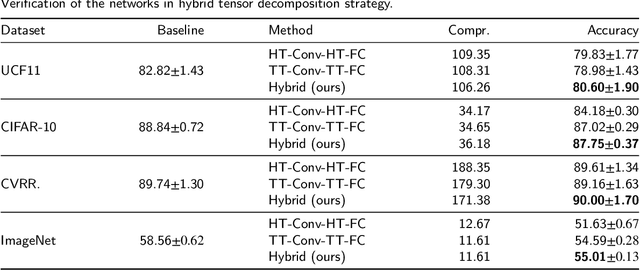
Deep neural networks (DNNs) have enabled impressive breakthroughs in various artificial intelligence (AI) applications recently due to its capability of learning high-level features from big data. However, the current demand of DNNs for computational resources especially the storage consumption is growing due to that the increasing sizes of models are being required for more and more complicated applications. To address this problem, several tensor decomposition methods including tensor-train (TT) and tensor-ring (TR) have been applied to compress DNNs and shown considerable compression effectiveness. In this work, we introduce the hierarchical Tucker (HT), a classical but rarely-used tensor decomposition method, to investigate its capability in neural network compression. We convert the weight matrices and convolutional kernels to both HT and TT formats for comparative study, since the latter is the most widely used decomposition method and the variant of HT. We further theoretically and experimentally discover that the HT format has better performance on compressing weight matrices, while the TT format is more suited for compressing convolutional kernels. Based on this phenomenon we propose a strategy of hybrid tensor decomposition by combining TT and HT together to compress convolutional and fully connected parts separately and attain better accuracy than only using the TT or HT format on convolutional neural networks (CNNs). Our work illuminates the prospects of hybrid tensor decomposition for neural network compression.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge