Communication-Computation Efficient Secure Aggregation for Federated Learning

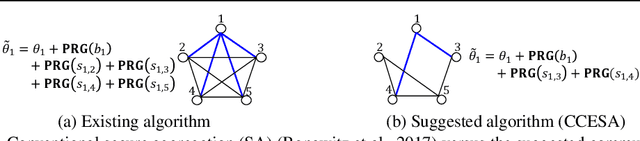
Federated learning has been spotlighted as a way to train neural networks using data distributed over multiple nodes without the need for the nodes to share data. Unfortunately, it has also been shown that data privacy could not be fully guaranteed as adversaries may be able to extract certain information on local data from the model parameters transmitted during federated learning. A recent solution based on the secure aggregation primitive enabled privacy-preserving federated learning, but at the expense of significant extra communication/computational resources. In this paper, we propose communication-computation efficient secure aggregation which substantially reduces the amount of communication/computational resources relative to the existing secure solution without sacrificing data privacy. The key idea behind the suggested scheme is to design the topology of the secret-sharing nodes as sparse random graphs instead of the complete graph corresponding to the existing solution. We first obtain the necessary and sufficient condition on the graph to guarantee reliable and private federated learning in the information-theoretic sense. We then suggest using the Erd\H{o}s-R\'enyi graph in particular and provide theoretical guarantees on the reliability/privacy of the proposed scheme. Through extensive real-world experiments, we demonstrate that our scheme, using only $20 \sim 30\%$ of the resources required in the conventional scheme, maintains virtually the same levels of reliability and data privacy in practical federated learning systems.

Election Coding for Distributed Learning: Protecting SignSGD against Byzantine Attacks

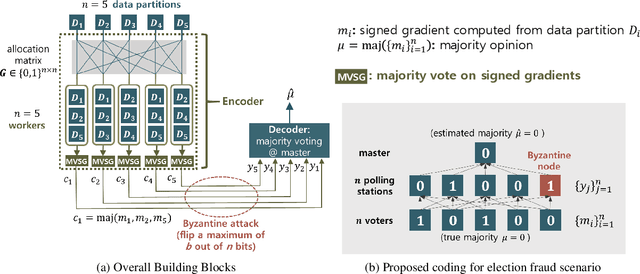
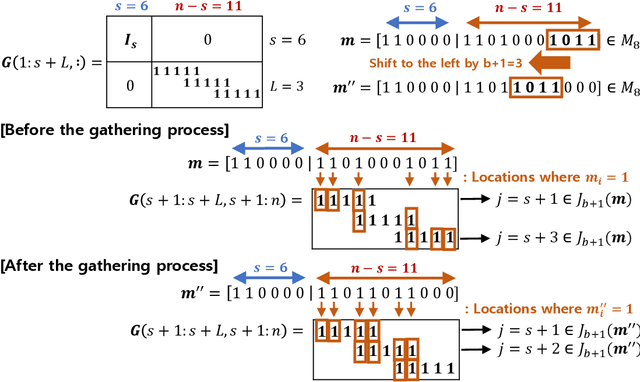
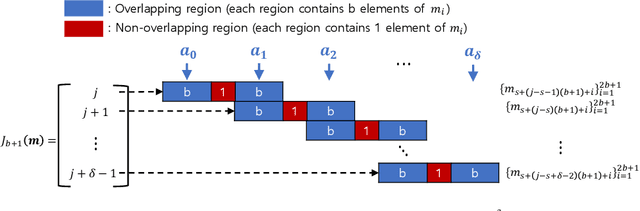
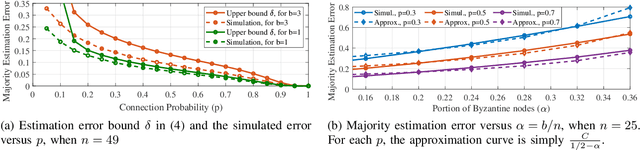
Recent advances in large-scale distributed learning algorithms have enabled communication-efficient training via SIGNSGD. Unfortunately, a major issue continues to plague distributed learning: namely, Byzantine failures may incur serious degradation in learning accuracy. This paper proposes ELECTION CODING, a coding-theoretic framework to guarantee Byzantine-robustness for SIGNSGD WITH MAJORITY VOTE, which uses minimum worker-master communication in both directions. The suggested framework explores new information-theoretic limits of finding the majority opinion when some workers could be malicious, and paves the road to implement robust and efficient distributed learning algorithms. Under this framework, we construct two types of explicit codes, random Bernoulli codes and deterministic algebraic codes, that can tolerate Byzantine attacks with a controlled amount of computational redundancy. For the Bernoulli codes, we provide upper bounds on the error probability in estimating the majority opinion, which give useful insights into code design for tolerating Byzantine attacks. As for deterministic codes, we construct an explicit code which perfectly tolerates Byzantines, and provide tight upper/lower bounds on the minimum required computational redundancy. Finally, the Byzantine-tolerance of the suggested coding schemes is confirmed by deep learning experiments on Amazon EC2 using Python with MPI4py package.