Communication-Computation Efficient Secure Aggregation for Federated Learning

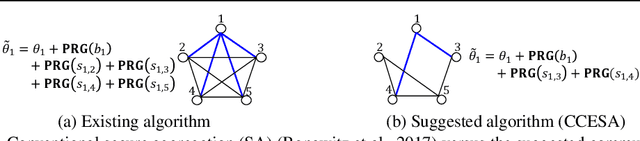
Federated learning has been spotlighted as a way to train neural networks using data distributed over multiple nodes without the need for the nodes to share data. Unfortunately, it has also been shown that data privacy could not be fully guaranteed as adversaries may be able to extract certain information on local data from the model parameters transmitted during federated learning. A recent solution based on the secure aggregation primitive enabled privacy-preserving federated learning, but at the expense of significant extra communication/computational resources. In this paper, we propose communication-computation efficient secure aggregation which substantially reduces the amount of communication/computational resources relative to the existing secure solution without sacrificing data privacy. The key idea behind the suggested scheme is to design the topology of the secret-sharing nodes as sparse random graphs instead of the complete graph corresponding to the existing solution. We first obtain the necessary and sufficient condition on the graph to guarantee reliable and private federated learning in the information-theoretic sense. We then suggest using the Erd\H{o}s-R\'enyi graph in particular and provide theoretical guarantees on the reliability/privacy of the proposed scheme. Through extensive real-world experiments, we demonstrate that our scheme, using only $20 \sim 30\%$ of the resources required in the conventional scheme, maintains virtually the same levels of reliability and data privacy in practical federated learning systems.