Election Coding for Distributed Learning: Protecting SignSGD against Byzantine Attacks
Paper and Code
Oct 14, 2019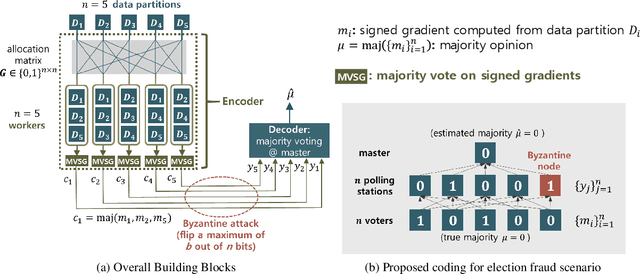
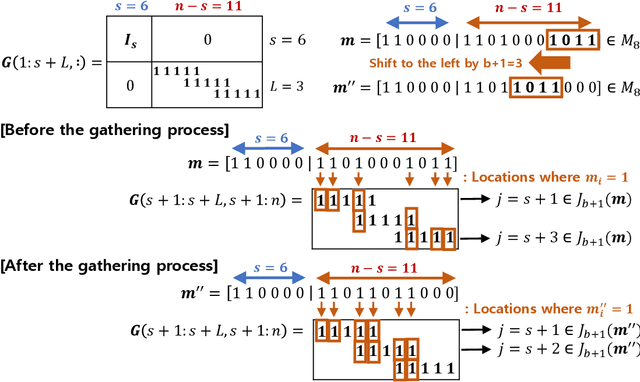
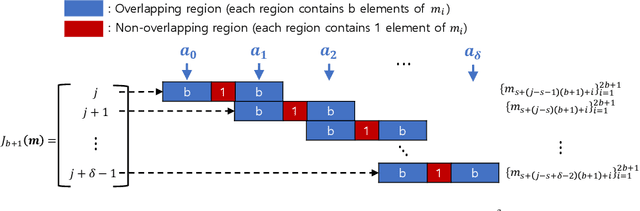
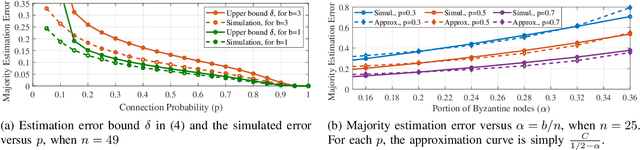
Recent advances in large-scale distributed learning algorithms have enabled communication-efficient training via SIGNSGD. Unfortunately, a major issue continues to plague distributed learning: namely, Byzantine failures may incur serious degradation in learning accuracy. This paper proposes ELECTION CODING, a coding-theoretic framework to guarantee Byzantine-robustness for SIGNSGD WITH MAJORITY VOTE, which uses minimum worker-master communication in both directions. The suggested framework explores new information-theoretic limits of finding the majority opinion when some workers could be malicious, and paves the road to implement robust and efficient distributed learning algorithms. Under this framework, we construct two types of explicit codes, random Bernoulli codes and deterministic algebraic codes, that can tolerate Byzantine attacks with a controlled amount of computational redundancy. For the Bernoulli codes, we provide upper bounds on the error probability in estimating the majority opinion, which give useful insights into code design for tolerating Byzantine attacks. As for deterministic codes, we construct an explicit code which perfectly tolerates Byzantines, and provide tight upper/lower bounds on the minimum required computational redundancy. Finally, the Byzantine-tolerance of the suggested coding schemes is confirmed by deep learning experiments on Amazon EC2 using Python with MPI4py package.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge