Robust Data-Driven Output Feedback Control via Bootstrapped Multiplicative Noise

We propose a robust data-driven output feedback control algorithm that explicitly incorporates inherent finite-sample model estimate uncertainties into the control design. The algorithm has three components: (1) a subspace identification nominal model estimator; (2) a bootstrap resampling method that quantifies non-asymptotic variance of the nominal model estimate; and (3) a non-conventional robust control design method comprising a coupled optimal dynamic output feedback filter and controller with multiplicative noise. A key advantage of the proposed approach is that the system identification and robust control design procedures both use stochastic uncertainty representations, so that the actual inherent statistical estimation uncertainty directly aligns with the uncertainty the robust controller is being designed against. Moreover, the control design method accommodates a highly structured uncertainty representation that can capture uncertainty shape more effectively than existing approaches. We show through numerical experiments that the proposed robust data-driven output feedback controller can significantly outperform a certainty equivalent controller on various measures of sample complexity and stability robustness.

Centralized Collision-free Polynomial Trajectories and Goal Assignment for Aerial Swarms

Computationally tractable methods are developed for centralized goal assignment and planning of collision-free polynomial-in-time trajectories for systems of multiple aerial robots. The method first assigns robots to goals to minimize total time-in-motion based on initial trajectories. By coupling the assignment and trajectory generation, the initial motion plans tend to require only limited collision resolution. The plans are then refined by checking for potential collisions and resolving them using either start time delays or altitude assignment. Numerical experiments using both methods show significant reductions in the total time required for agents to arrive at goals with only modest additional computational effort in comparison to state-of-the-art prior work, enabling planning for thousands of agents.

Approximate Midpoint Policy Iteration for Linear Quadratic Control

We present a midpoint policy iteration algorithm to solve linear quadratic optimal control problems in both model-based and model-free settings. The algorithm is a variation of Newton's method, and we show that in the model-based setting it achieves cubic convergence, which is superior to standard policy iteration and policy gradient algorithms that achieve quadratic and linear convergence, respectively. We also demonstrate that the algorithm can be approximately implemented without knowledge of the dynamics model by using least-squares estimates of the state-action value function from trajectory data, from which policy improvements can be obtained. With sufficient trajectory data, the policy iterates converge cubically to approximately optimal policies, and this occurs with the same available sample budget as the approximate standard policy iteration. Numerical experiments demonstrate effectiveness of the proposed algorithms.

Robust Learning-Based Control via Bootstrapped Multiplicative Noise

Despite decades of research and recent progress in adaptive control and reinforcement learning, there remains a fundamental lack of understanding in designing controllers that provide robustness to inherent non-asymptotic uncertainties arising from models estimated with finite, noisy data. We propose a robust adaptive control algorithm that explicitly incorporates such non-asymptotic uncertainties into the control design. The algorithm has three components: (1) a least-squares nominal model estimator; (2) a bootstrap resampling method that quantifies non-asymptotic variance of the nominal model estimate; and (3) a non-conventional robust control design method using an optimal linear quadratic regulator (LQR) with multiplicative noise. A key advantage of the proposed approach is that the system identification and robust control design procedures both use stochastic uncertainty representations, so that the actual inherent statistical estimation uncertainty directly aligns with the uncertainty the robust controller is being designed against. We show through numerical experiments that the proposed robust adaptive controller can significantly outperform the certainty equivalent controller on both expected regret and measures of regret risk.

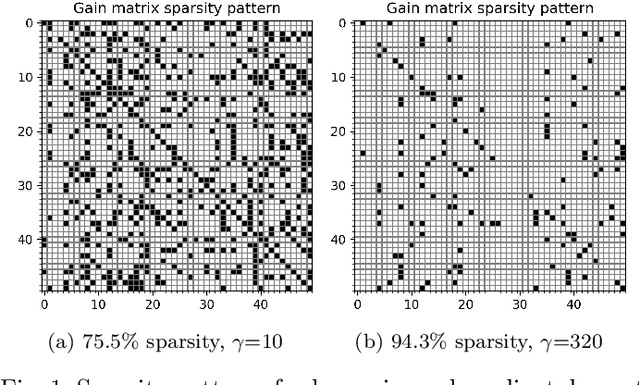
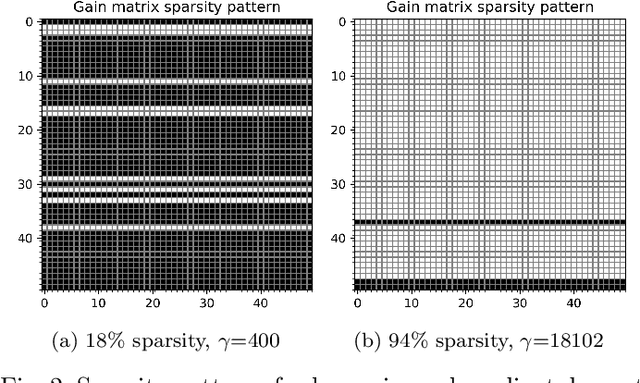
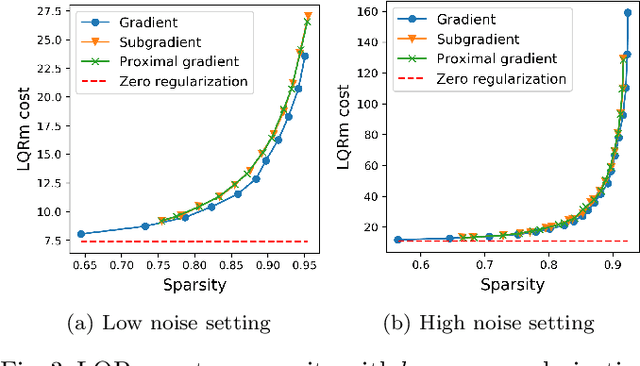
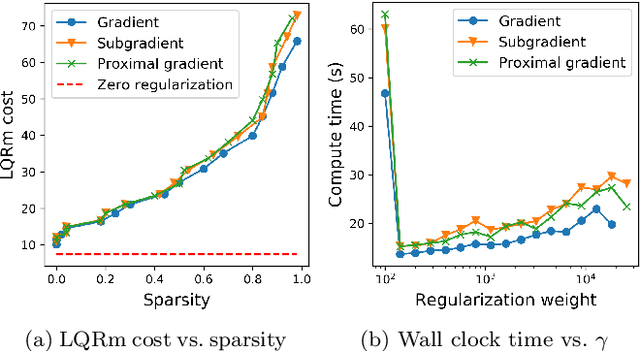
Sparse optimal control of networks with multiplicative noise via policy gradient

We give algorithms for designing near-optimal sparse controllers using policy gradient with applications to control of systems corrupted by multiplicative noise, which is increasingly important in emerging complex dynamical networks. Various regularization schemes are examined and incorporated into the optimization by the use of gradient, subgradient, and proximal gradient methods. Numerical experiments on a large networked system show that the algorithms converge to performant sparse mean-square stabilizing controllers.

Learning robust control for LQR systems with multiplicative noise via policy gradient

The linear quadratic regulator (LQR) problem has reemerged as an important theoretical benchmark for reinforcement learning-based control of complex dynamical systems with continuous state and action spaces. In contrast with nearly all recent work in this area, we consider multiplicative noise models, which are increasingly relevant because they explicitly incorporate inherent uncertainty and variation in the system dynamics and thereby improve robustness properties of the controller. Robustness is a critical and poorly understood issue in reinforcement learning; existing methods which do not account for uncertainty can converge to fragile policies or fail to converge at all. Additionally, intentional injection of multiplicative noise into learning algorithms can enhance robustness of policies, as observed in ad hoc work on domain randomization. Although policy gradient algorithms require optimization of a non-convex cost function, we show that the multiplicative noise LQR cost has a special property called gradient domination, which is exploited to prove global convergence of policy gradient algorithms to the globally optimum control policy with polynomial dependence on problem parameters. Results are provided both in the model-known and model-unknown settings where samples of system trajectories are used to estimate policy gradients.