Sparse optimal control of networks with multiplicative noise via policy gradient
Paper and Code
May 28, 2019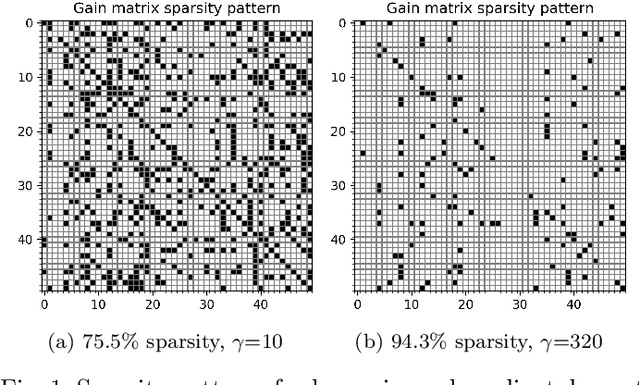
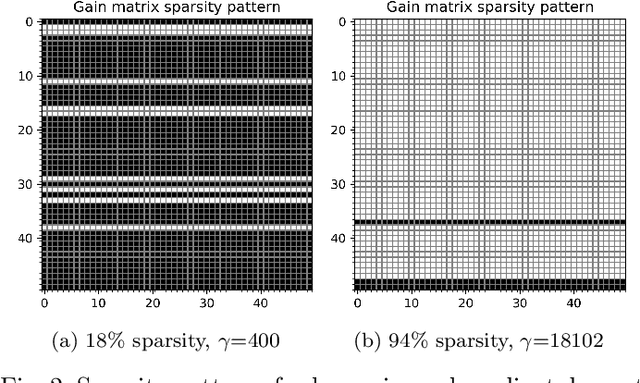
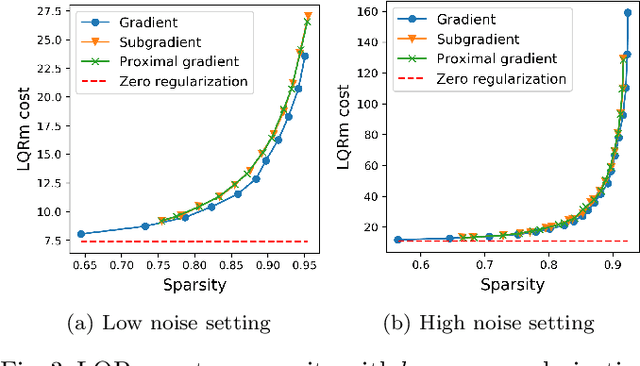
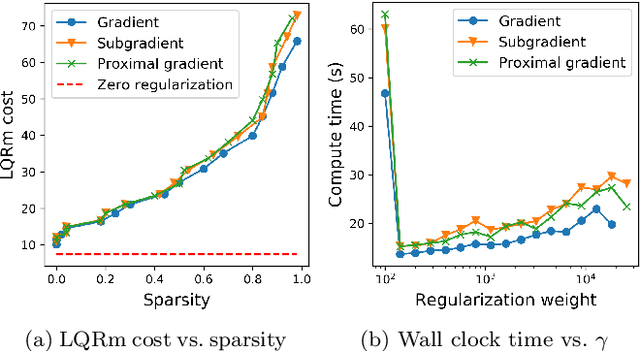
We give algorithms for designing near-optimal sparse controllers using policy gradient with applications to control of systems corrupted by multiplicative noise, which is increasingly important in emerging complex dynamical networks. Various regularization schemes are examined and incorporated into the optimization by the use of gradient, subgradient, and proximal gradient methods. Numerical experiments on a large networked system show that the algorithms converge to performant sparse mean-square stabilizing controllers.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge