Joint Graph and Vertex Importance Learning

In this paper, we explore the topic of graph learning from the perspective of the Irregularity-Aware Graph Fourier Transform, with the goal of learning the graph signal space inner product to better model data. We propose a novel method to learn a graph with smaller edge weight upper bounds compared to combinatorial Laplacian approaches. Experimentally, our approach yields much sparser graphs compared to a combinatorial Laplacian approach, with a more interpretable model.

Two Channel Filter Banks on Arbitrary Graphs with Positive Semi Definite Variation Operators

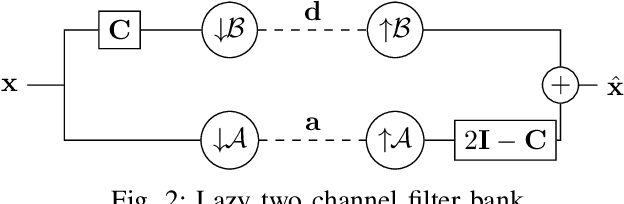
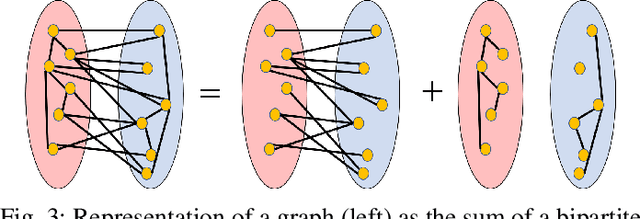
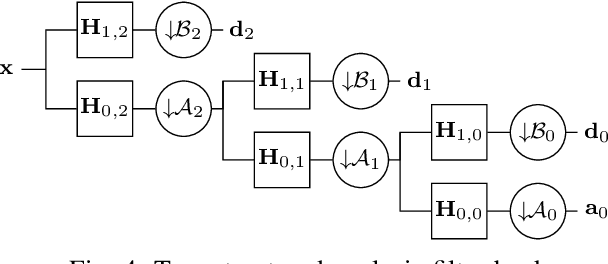
We study the design of filter banks for signals defined on the nodes of graphs. We propose novel two channel filter banks, that can be applied to arbitrary graphs, given a positive semi definite variation operator, while using downsampling operators on arbitrary vertex partitions. The proposed filter banks also satisfy several desirable properties, including perfect reconstruction, and critical sampling, while having efficient implementations. Our results generalize previous approaches only valid for the normalized Laplacian of bipartite graphs. We consider graph Fourier transforms (GFTs) given by the generalized eigenvectors of the variation operator. This GFT basis is orthogonal in an alternative inner product space, which depends on the choices of downsampling sets and variation operators. We show that the spectral folding property of the normalized Laplacian of bipartite graphs, at the core of bipartite filter bank theory, can be generalized for the proposed GFT if the inner product matrix is chosen properly. We give a probabilistic interpretation to the proposed filter banks using Gaussian graphical models. We also study orthogonality properties of tree structured filter banks, and propose a vertex partition algorithm for downsampling. We show that the proposed filter banks can be implemented efficiently on 3D point clouds, with hundreds of thousands of points (nodes), while also improving the color signal representation quality over competing state of the art approaches.

Region adaptive graph fourier transform for 3d point clouds

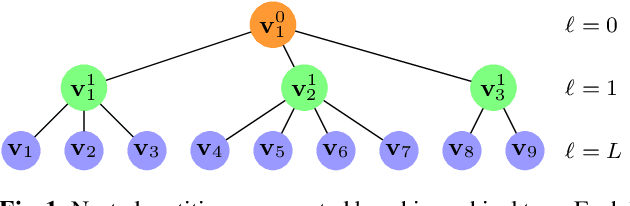
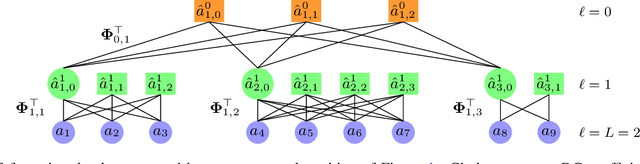
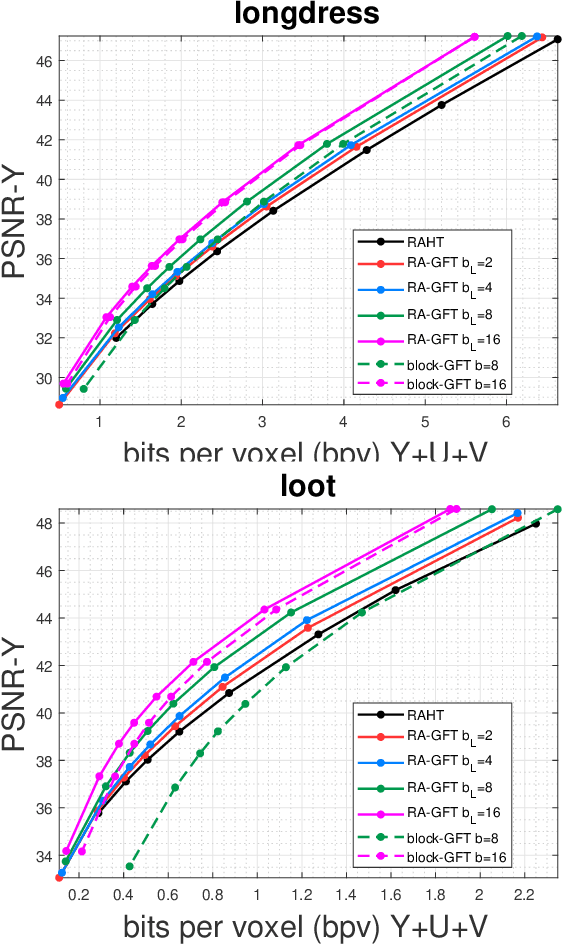
We introduce the Region Adaptive Graph Fourier Transform (RA-GFT) for compression of 3D point cloud attributes. We assume the points are organized by a family of nested partitions represented by a tree. The RA-GFT is a multiresolution transform, formed by combining spatially localized block transforms. At each resolution level, attributes are processed in clusters by a set of block transforms. Each block transform produces a single approximation (DC) coefficient, and various detail (AC) coefficients. The DC coefficients are promoted up the tree to the next (lower resolution) level, where the process can be repeated until reaching the root. Since clusters may have a different numbers of points, each block transform must incorporate the relative importance of each coefficient. For this, we introduce the $\mathbf{Q}$-normalized graph Laplacian, and propose using its eigenvectors as the block transform. The RA-GFT outperforms the Region Adaptive Haar Transform (RAHT) by up to 2.5 dB, with a small complexity overhead.

Generating Labels for Regression of Subjective Constructs using Triplet Embeddings

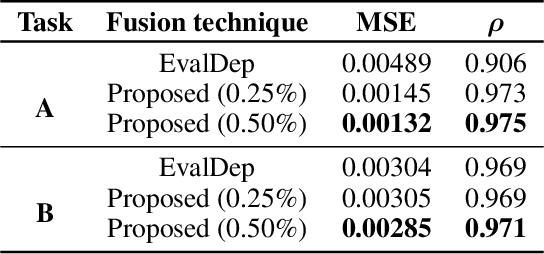
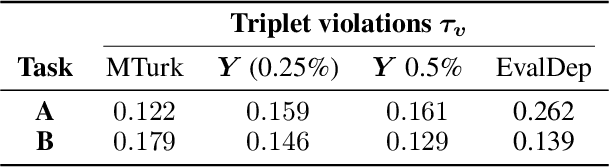
Human annotations serve an important role in computational models where the target constructs under study are hidden, such as dimensions of affect. This is especially relevant in machine learning, where subjective labels derived from related observable signals (e.g., audio, video, text) are needed to support model training and testing. Current research trends focus on correcting artifacts and biases introduced by annotators during the annotation process while fusing them into a single annotation. In this work, we propose a novel annotation approach using triplet embeddings. By lifting the absolute annotation process to relative annotations where the annotator compares individual target constructs in triplets, we leverage the accuracy of comparisons over absolute ratings by human annotators. We then build a 1-dimensional embedding in Euclidean space that is indexed in time and serves as a label for regression. In this setting, the annotation fusion occurs naturally as a union of sets of sampled triplet comparisons among different annotators. We show that by using our proposed sampling method to find an embedding, we are able to accurately represent synthetic hidden constructs in time under noisy sampling conditions. We further validate this approach using human annotations collected from Mechanical Turk and show that we can recover the underlying structure of the hidden construct up to bias and scaling factors.