Region adaptive graph fourier transform for 3d point clouds
Paper and Code
Mar 04, 2020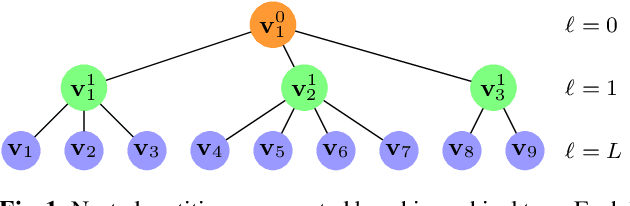

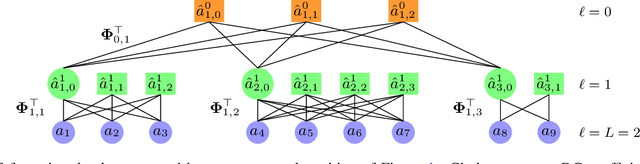
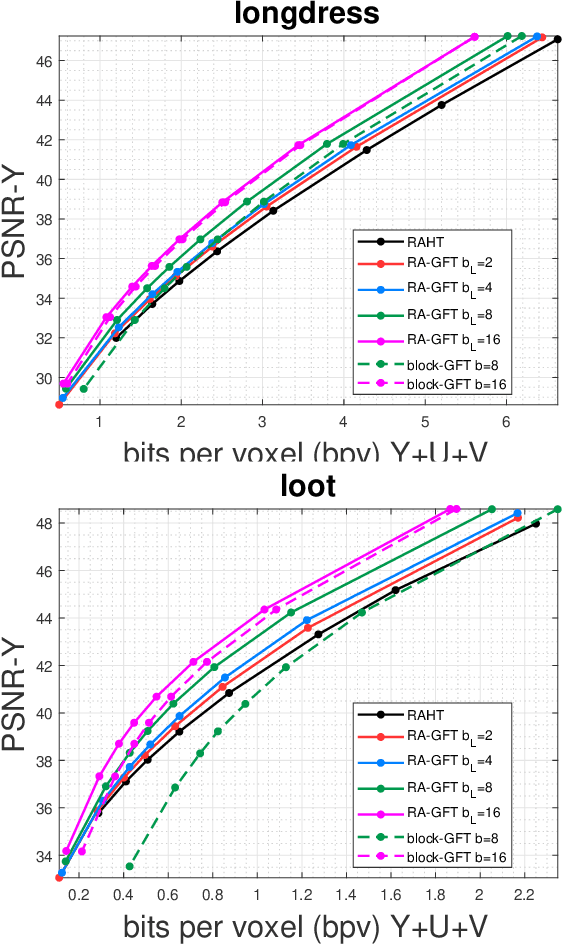
We introduce the Region Adaptive Graph Fourier Transform (RA-GFT) for compression of 3D point cloud attributes. We assume the points are organized by a family of nested partitions represented by a tree. The RA-GFT is a multiresolution transform, formed by combining spatially localized block transforms. At each resolution level, attributes are processed in clusters by a set of block transforms. Each block transform produces a single approximation (DC) coefficient, and various detail (AC) coefficients. The DC coefficients are promoted up the tree to the next (lower resolution) level, where the process can be repeated until reaching the root. Since clusters may have a different numbers of points, each block transform must incorporate the relative importance of each coefficient. For this, we introduce the $\mathbf{Q}$-normalized graph Laplacian, and propose using its eigenvectors as the block transform. The RA-GFT outperforms the Region Adaptive Haar Transform (RAHT) by up to 2.5 dB, with a small complexity overhead.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge