Benjamin Dutton
Adversarial Canonical Correlation Analysis
Jun 09, 2020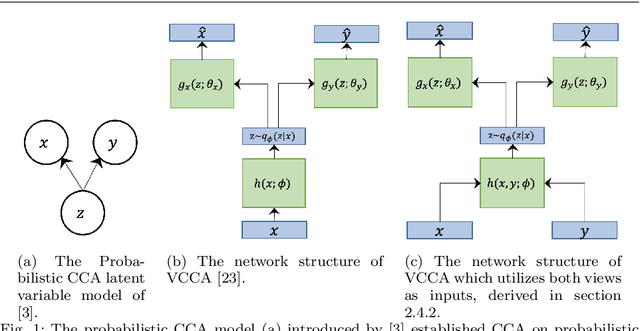
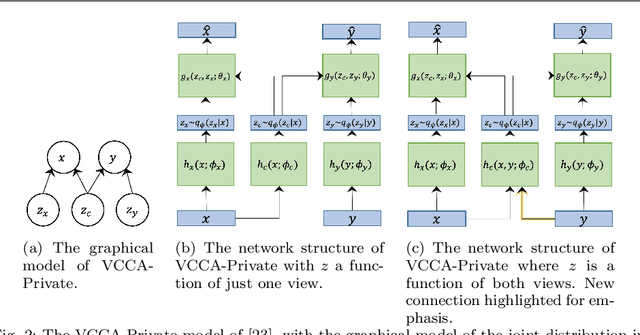
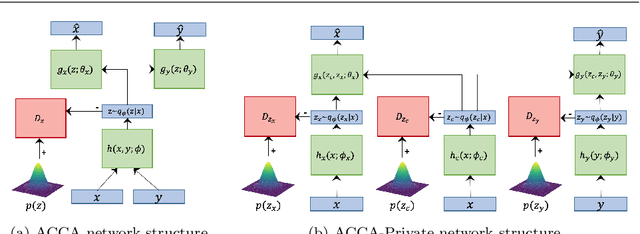

Abstract:Canonical Correlation Analysis (CCA) is a statistical technique used to extract common information from multiple data sources or views. It has been used in various representation learning problems, such as dimensionality reduction, word embedding, and clustering. Recent work has given CCA probabilistic footing in a deep learning context and uses a variational lower bound for the data log likelihood to estimate model parameters. Alternatively, adversarial techniques have arisen in recent years as a powerful alternative to variational Bayesian methods in autoencoders. In this work, we explore straightforward adversarial alternatives to recent work in Deep Variational CCA (VCCA and VCCA-Private) we call ACCA and ACCA-Private and show how these approaches offer a stronger and more flexible way to match the approximate posteriors coming from encoders to much larger classes of priors than the VCCA and VCCA-Private models. This allows new priors for what constitutes a good representation, such as disentangling underlying factors of variation, to be more directly pursued. We offer further analysis on the multi-level disentangling properties of VCCA-Private and ACCA-Private through the use of a newly designed dataset we call Tangled MNIST. We also design a validation criteria for these models that is theoretically grounded, task-agnostic, and works well in practice. Lastly, we fill a minor research gap by deriving an additional variational lower bound for VCCA that allows the representation to use view-specific information from both input views.
Local Clustering with Mean Teacher for Semi-supervised Learning
Apr 20, 2020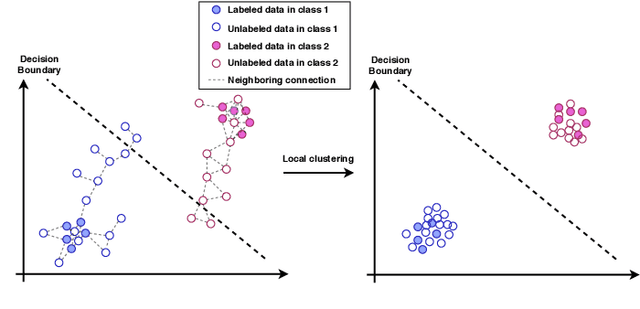
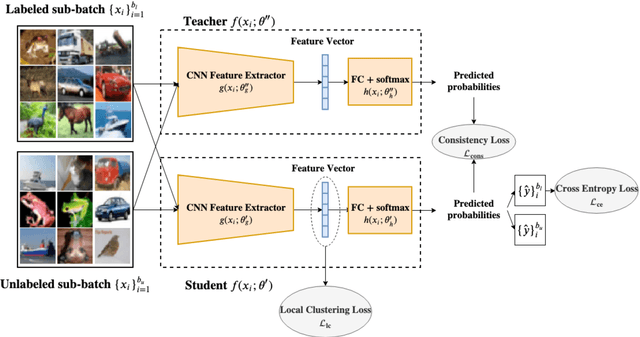
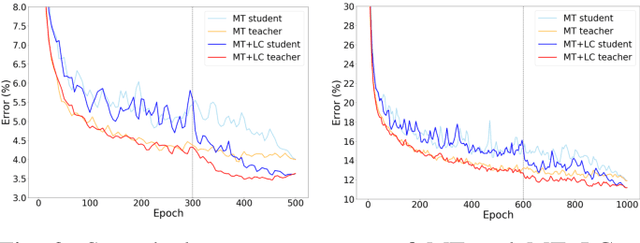

Abstract:The Mean Teacher (MT) model of Tarvainen and Valpola has shown favorable performance on several semi-supervised benchmark datasets. MT maintains a teacher model's weights as the exponential moving average of a student model's weights and minimizes the divergence between their probability predictions under diverse perturbations of the inputs. However, MT is known to suffer from confirmation bias, that is, reinforcing incorrect teacher model predictions. In this work, we propose a simple yet effective method called Local Clustering (LC) to mitigate the effect of confirmation bias. In MT, each data point is considered independent of other points during training; however, data points are likely to be close to each other in feature space if they share similar features. Motivated by this, we cluster data points locally by minimizing the pairwise distance between neighboring data points in feature space. Combined with a standard classification cross-entropy objective on labeled data points, the misclassified unlabeled data points are pulled towards high-density regions of their correct class with the help of their neighbors, thus improving model performance. We demonstrate on semi-supervised benchmark datasets SVHN and CIFAR-10 that adding our LC loss to MT yields significant improvements compared to MT and performance comparable to the state of the art in semi-supervised learning.
Estimating a Manifold from a Tangent Bundle Learner
Jun 18, 2019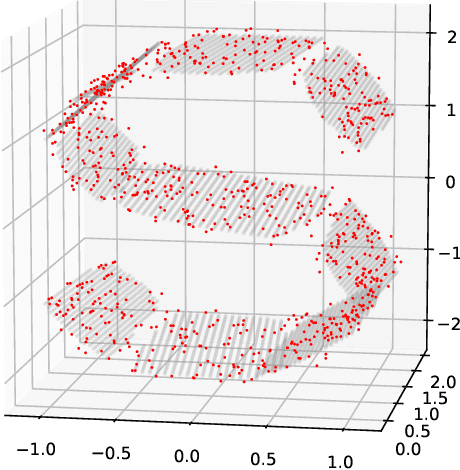
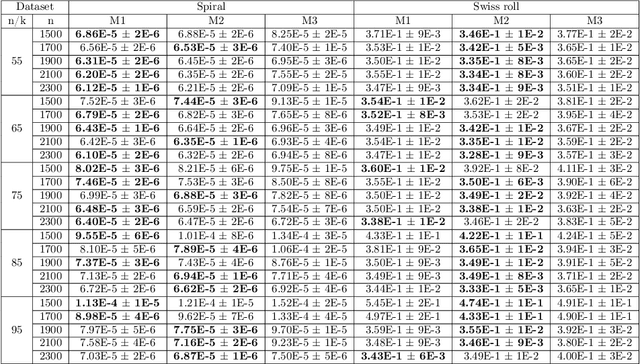
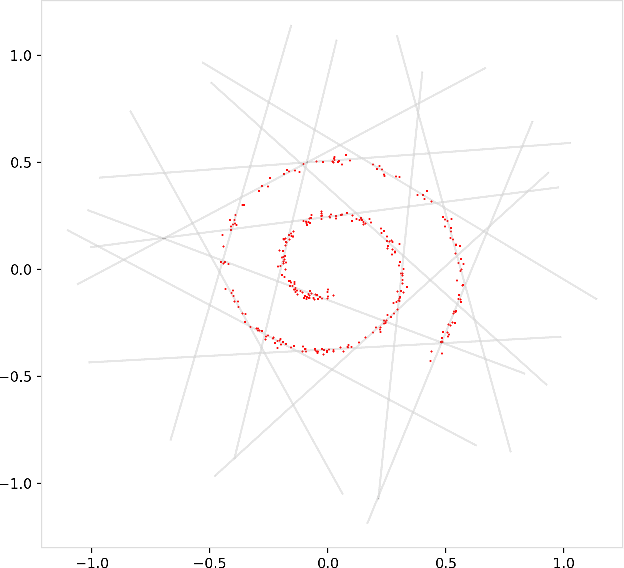
Abstract:Manifold hypotheses are typically used for tasks such as dimensionality reduction, interpolation, or improving classification performance. In the less common problem of manifold estimation, the task is to characterize the geometric structure of the manifold in the original ambient space from a sample. We focus on the role that tangent bundle learners (TBL) can play in estimating the underlying manifold from which data is assumed to be sampled. Since the unbounded tangent spaces natively represent a poor manifold estimate, the problem reduces to one of estimating regions in the tangent space where it acts as a relatively faithful linear approximator to the surface of the manifold. Local PCA methods, such as the Mixtures of Probabilistic Principal Component Analyzers method of Tipping and Bishop produce a subset of the tangent bundle of the manifold along with an assignment function that assigns points in the training data used by the TBL to elements of the estimated tangent bundle. We formulate three methods that use the data assigned to each tangent space to estimate the underlying bounded subspaces for which the tangent space is a faithful estimate of the manifold and offer thoughts on how this perspective is theoretically grounded in the manifold assumption. We seek to explore the conceptual and technical challenges that arise in trying to utilize simple TBL methods to arrive at reliable estimates of the underlying manifold.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge