Approximate Extraction of Late-Time Returns via Morphological Component Analysis

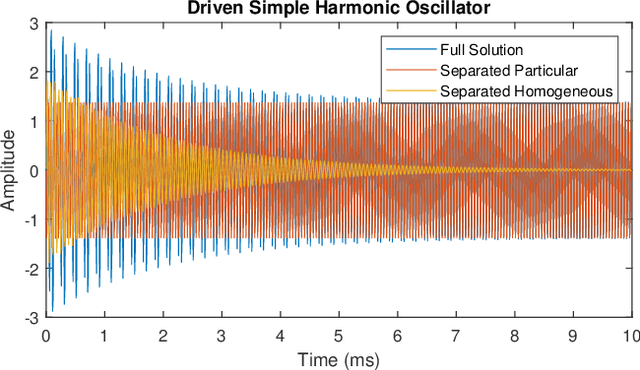
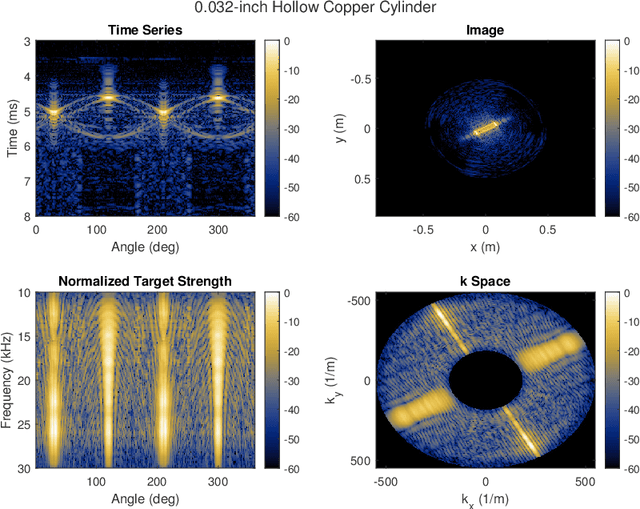
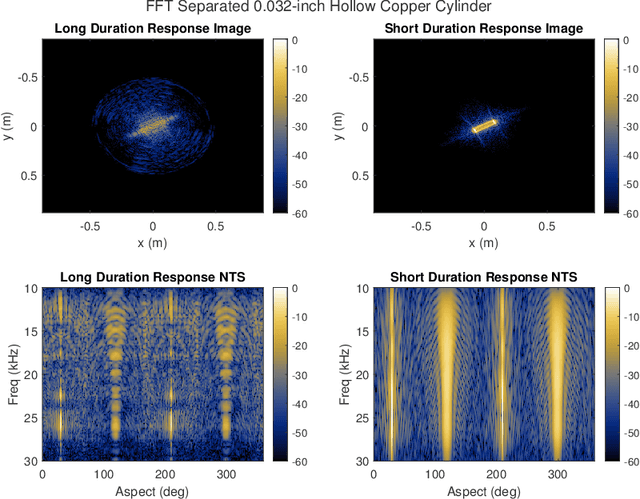
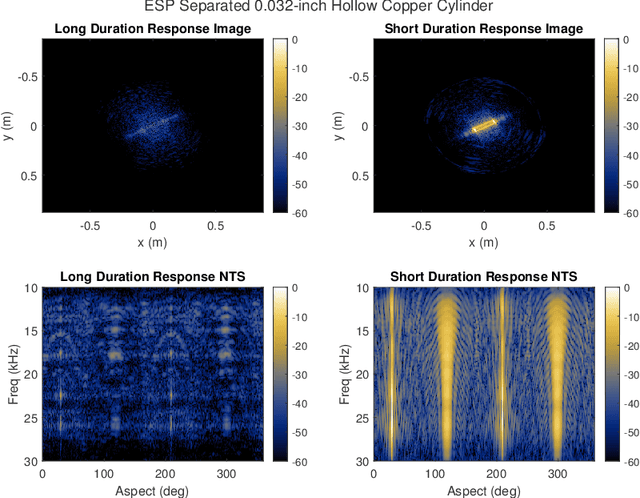
A fundamental challenge in acoustic data processing is to separate a measured time series into relevant phenomenological components. A given measurement is typically assumed to be an additive mixture of myriad signals plus noise whose separation forms an ill-posed inverse problem. In the setting of sensing elastic objects using active sonar, we wish to separate the early-time returns (e.g., returns from the object's exterior geometry) from late-time returns caused by elastic or compressional wave coupling. Under the framework of Morphological Component Analysis (MCA), we compare two separation models using the short-duration and long-duration responses as a proxy for early-time and late-time returns. Results are computed for Stanton's elastic cylinder model as well as on experimental data taken from an in-Air circular Synthetic Aperture Sonar (AirSAS) system, whose separated time series are formed into imagery. We find that MCA can be used to separate early and late-time responses in both cases without the use of time-gating. The separation process is demonstrated to be robust to noise and compatible with AirSAS image reconstruction. The best separation results are obtained with a flexible, but computationally intensive, frame based signal model, while a faster Fourier Transform based method is shown to have competitive performance.

Enveloped Sinusoid Parseval Frames

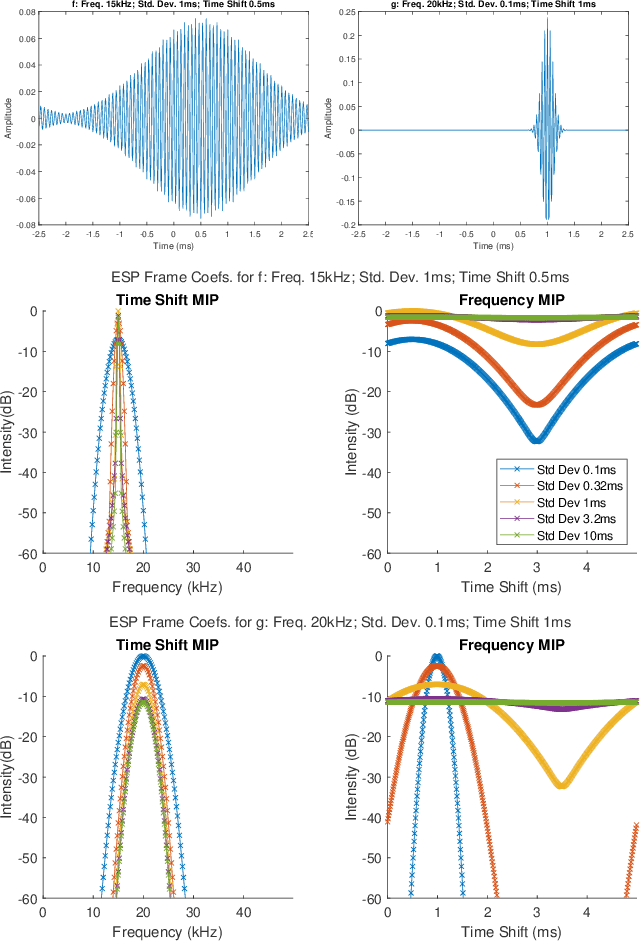
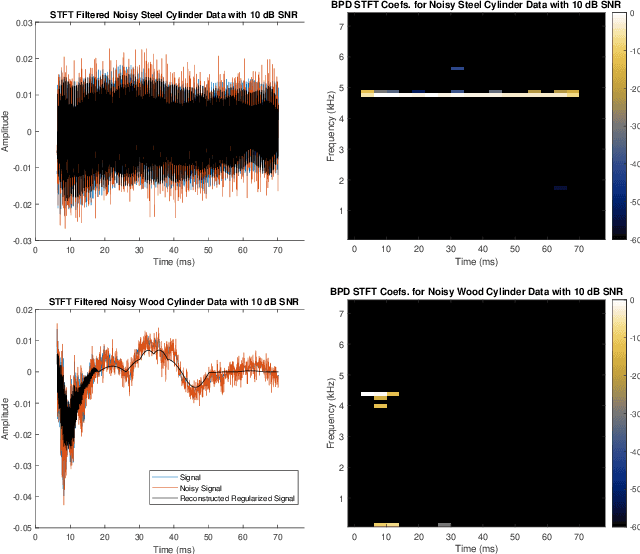
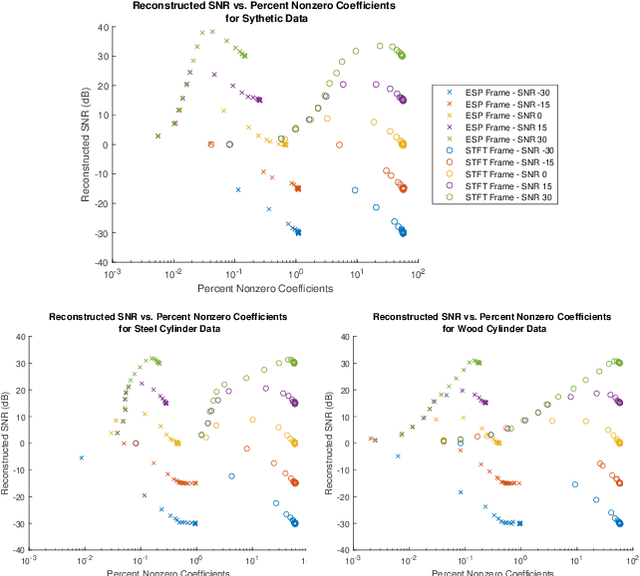
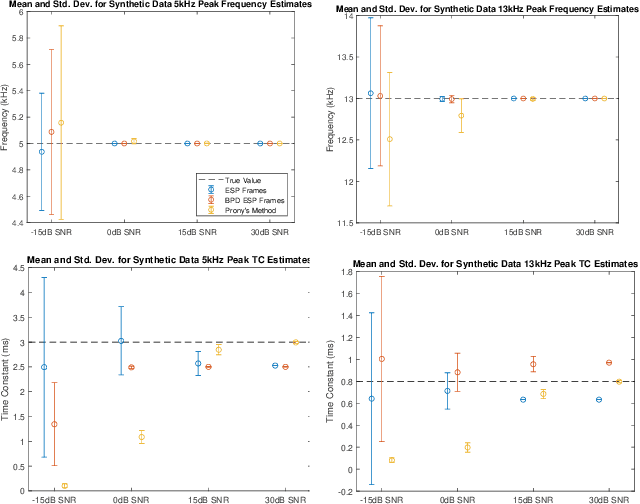
This paper presents a method of constructing Parseval frames from any collection of complex envelopes. The resulting Enveloped Sinusoid Parseval (ESP) frames can represent a wide variety of signal types as specified by their physical morphology. Since the ESP frame retains its Parseval property even when generated from a variety of envelopes, it is compatible with large scale and iterative optimization algorithms. ESP frames are constructed by applying time-shifted enveloping functions to the discrete Fourier Transform basis, and in this way are similar to the short-time Fourier Transform. This work provides examples of ESP frame generation for both synthetic and experimentally measured signals. Furthermore, the frame's compatibility with distributed sparse optimization frameworks is demonstrated, and efficient implementation details are provided. Numerical experiments on acoustics data reveal that the flexibility of this method allows it to be simultaneously competitive with the STFT in time-frequency processing and also with Prony's Method for time-constant parameter estimation, surpassing the shortcomings of each individual technique.

LSALSA: efficient sparse coding in single and multiple dictionary settings

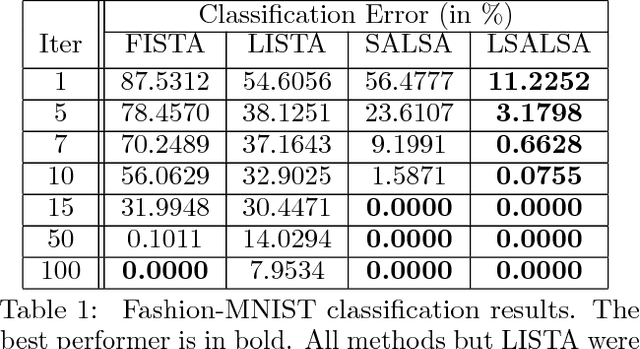
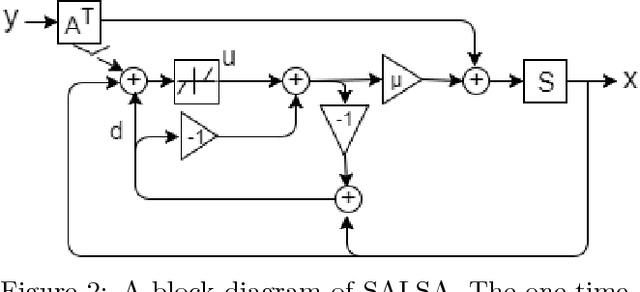
We propose an efficient sparse coding (SC) framework for obtaining sparse representation of data. The proposed framework is very general and applies to both the single dictionary setting, where each data point is represented as a sparse combination of the columns of one dictionary matrix, as well as the multiple dictionary setting as given in morphological component analysis (MCA), where the goal is to separate the data into additive parts such that each part has distinct sparse representation within an appropriately chosen corresponding dictionary. Both tasks have been cast as $\ell_1$-regularized optimization problems of minimizing quadratic reconstruction error. In an effort to accelerate traditional acquisition of sparse codes, we propose a deep learning architecture that constitutes a trainable time-unfolded version of the Split Augmented Lagrangian Shrinkage Algorithm (SALSA), a special case of the alternating direction method of multipliers (ADMM). We empirically validate both variants of the algorithm on image vision tasks and demonstrate that at inference our networks achieve improvements in terms of the running time and the quality of estimated sparse codes on both classic SC and MCA problems over more common baselines. We finally demonstrate the visual advantage of our technique on the task of source separation.