Enveloped Sinusoid Parseval Frames
Paper and Code
Apr 18, 2022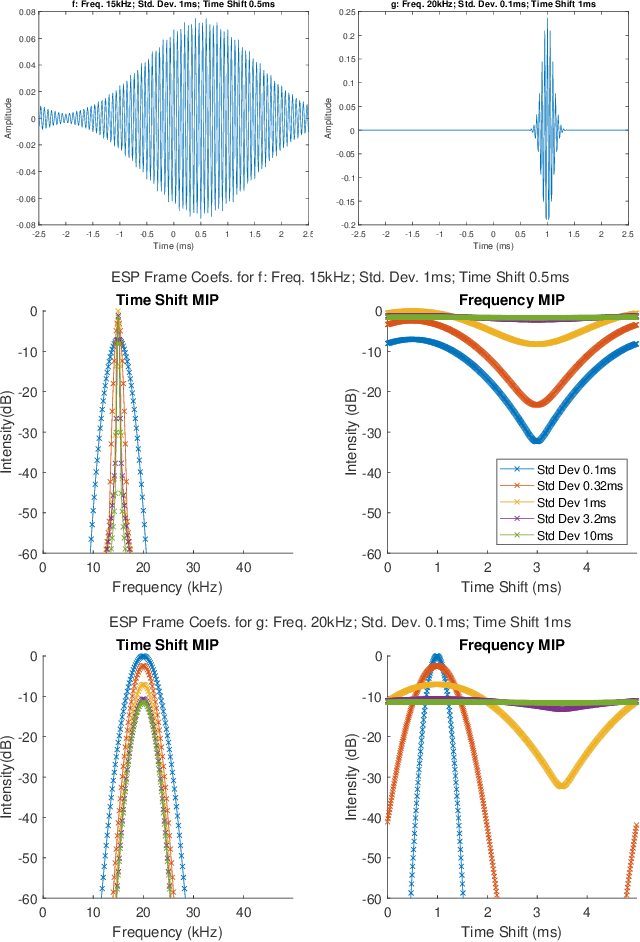
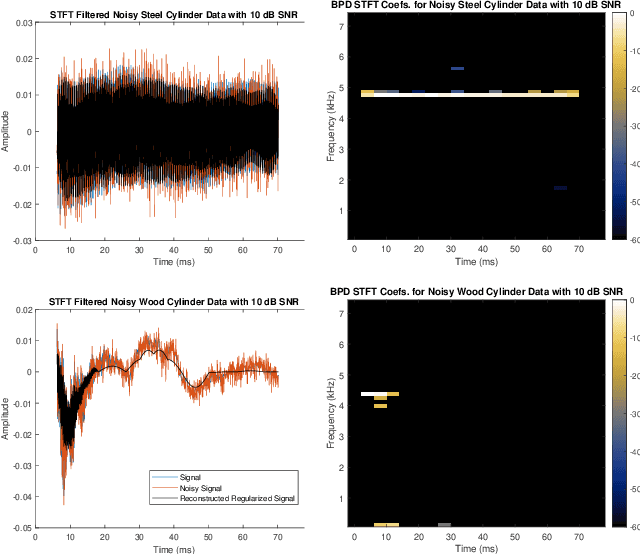
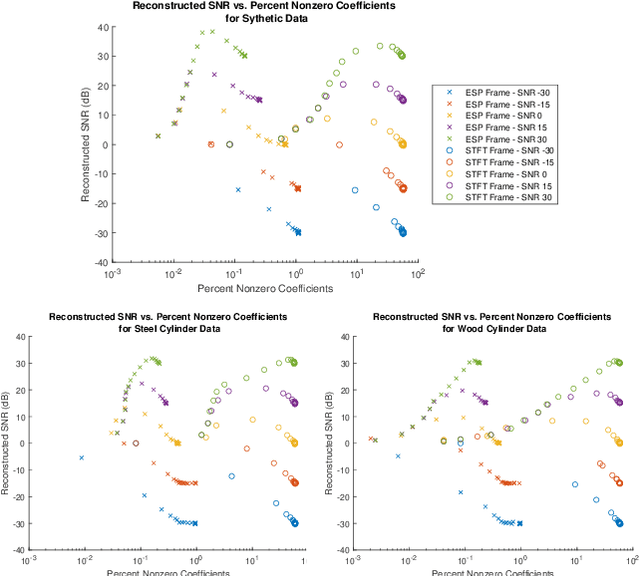
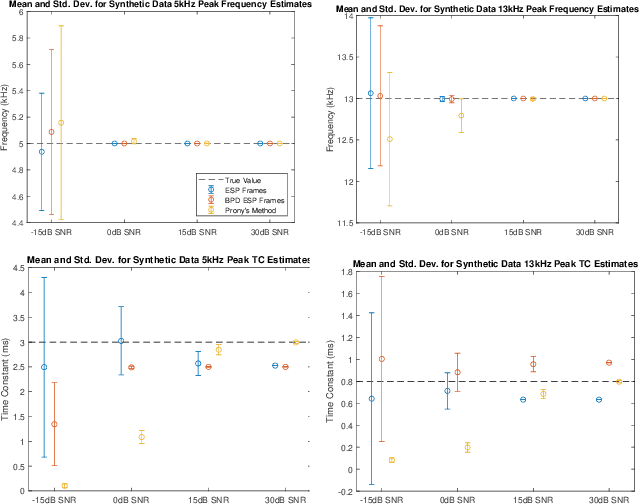
This paper presents a method of constructing Parseval frames from any collection of complex envelopes. The resulting Enveloped Sinusoid Parseval (ESP) frames can represent a wide variety of signal types as specified by their physical morphology. Since the ESP frame retains its Parseval property even when generated from a variety of envelopes, it is compatible with large scale and iterative optimization algorithms. ESP frames are constructed by applying time-shifted enveloping functions to the discrete Fourier Transform basis, and in this way are similar to the short-time Fourier Transform. This work provides examples of ESP frame generation for both synthetic and experimentally measured signals. Furthermore, the frame's compatibility with distributed sparse optimization frameworks is demonstrated, and efficient implementation details are provided. Numerical experiments on acoustics data reveal that the flexibility of this method allows it to be simultaneously competitive with the STFT in time-frequency processing and also with Prony's Method for time-constant parameter estimation, surpassing the shortcomings of each individual technique.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge