LSALSA: efficient sparse coding in single and multiple dictionary settings
Paper and Code
Feb 13, 2018
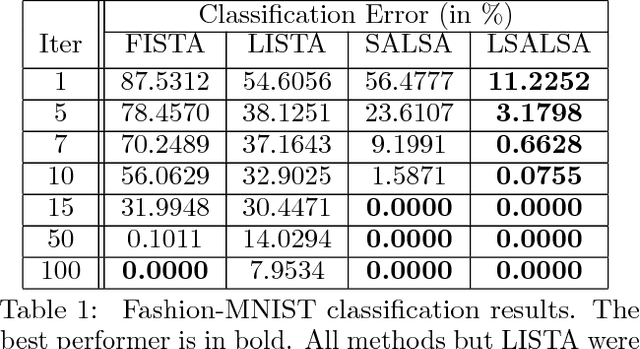
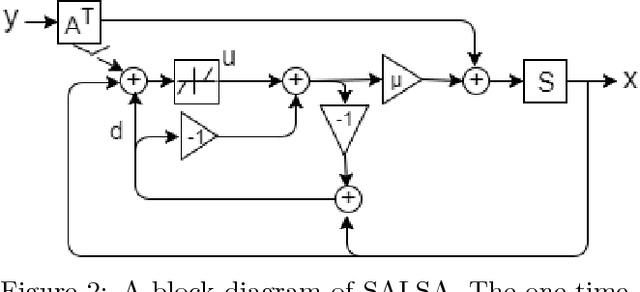

We propose an efficient sparse coding (SC) framework for obtaining sparse representation of data. The proposed framework is very general and applies to both the single dictionary setting, where each data point is represented as a sparse combination of the columns of one dictionary matrix, as well as the multiple dictionary setting as given in morphological component analysis (MCA), where the goal is to separate the data into additive parts such that each part has distinct sparse representation within an appropriately chosen corresponding dictionary. Both tasks have been cast as $\ell_1$-regularized optimization problems of minimizing quadratic reconstruction error. In an effort to accelerate traditional acquisition of sparse codes, we propose a deep learning architecture that constitutes a trainable time-unfolded version of the Split Augmented Lagrangian Shrinkage Algorithm (SALSA), a special case of the alternating direction method of multipliers (ADMM). We empirically validate both variants of the algorithm on image vision tasks and demonstrate that at inference our networks achieve improvements in terms of the running time and the quality of estimated sparse codes on both classic SC and MCA problems over more common baselines. We finally demonstrate the visual advantage of our technique on the task of source separation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge