A Unified Approach to Coreset Learning

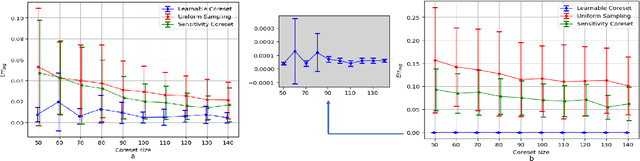
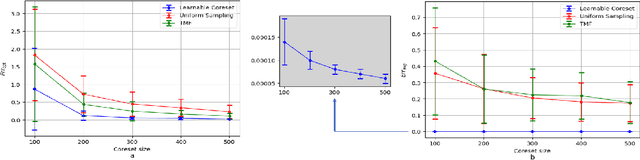
Coreset of a given dataset and loss function is usually a small weighed set that approximates this loss for every query from a given set of queries. Coresets have shown to be very useful in many applications. However, coresets construction is done in a problem dependent manner and it could take years to design and prove the correctness of a coreset for a specific family of queries. This could limit coresets use in practical applications. Moreover, small coresets provably do not exist for many problems. To address these limitations, we propose a generic, learning-based algorithm for construction of coresets. Our approach offers a new definition of coreset, which is a natural relaxation of the standard definition and aims at approximating the \emph{average} loss of the original data over the queries. This allows us to use a learning paradigm to compute a small coreset of a given set of inputs with respect to a given loss function using a training set of queries. We derive formal guarantees for the proposed approach. Experimental evaluation on deep networks and classic machine learning problems show that our learned coresets yield comparable or even better results than the existing algorithms with worst-case theoretical guarantees (that may be too pessimistic in practice). Furthermore, our approach applied to deep network pruning provides the first coreset for a full deep network, i.e., compresses all the network at once, and not layer by layer or similar divide-and-conquer methods.

Data-Independent Structured Pruning of Neural Networks via Coresets

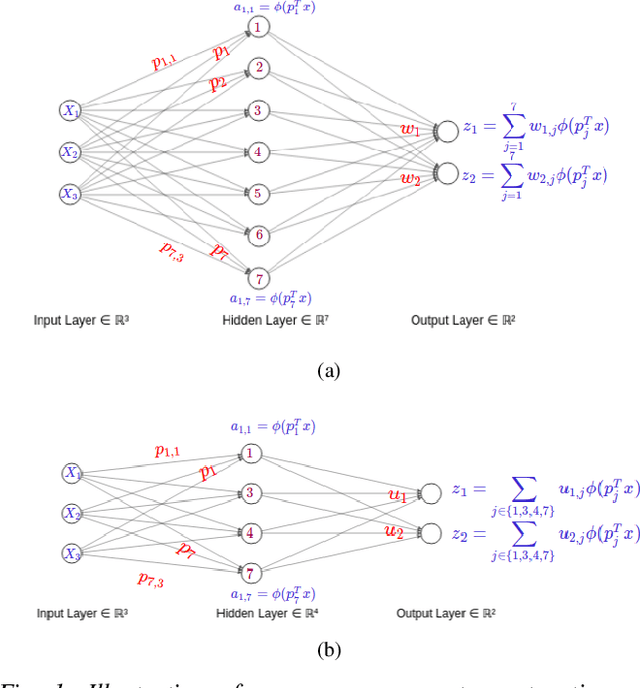
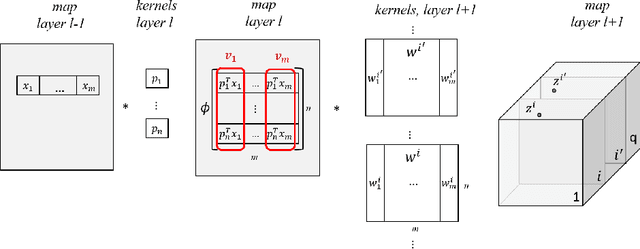
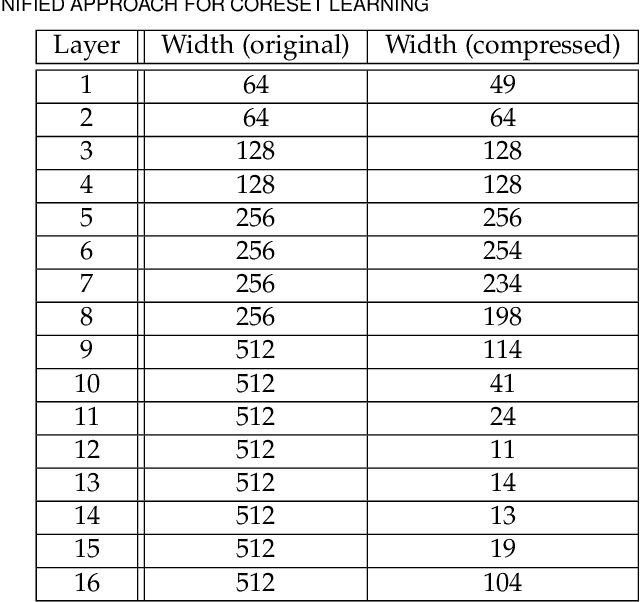
Model compression is crucial for deployment of neural networks on devices with limited computational and memory resources. Many different methods show comparable accuracy of the compressed model and similar compression rates. However, the majority of the compression methods are based on heuristics and offer no worst-case guarantees on the trade-off between the compression rate and the approximation error for an arbitrarily new sample. We propose the first efficient structured pruning algorithm with a provable trade-off between its compression rate and the approximation error for any future test sample. Our method is based on the coreset framework and it approximates the output of a layer of neurons/filters by a coreset of neurons/filters in the previous layer and discards the rest. We apply this framework in a layer-by-layer fashion from the bottom to the top. Unlike previous works, our coreset is data independent, meaning that it provably guarantees the accuracy of the function for any input $x\in \mathbb{R}^d$, including an adversarial one.

On Activation Function Coresets for Network Pruning

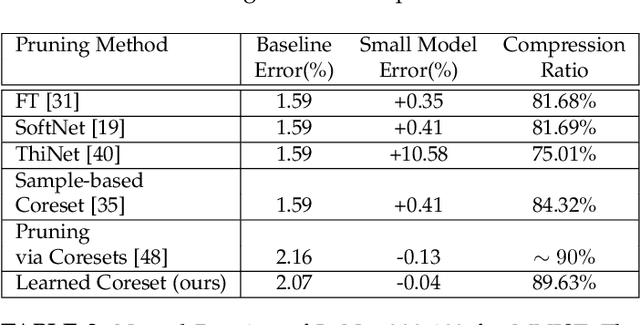
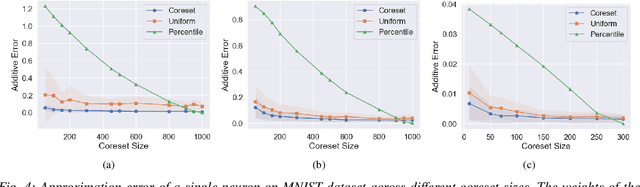
Model compression provides a means to efficiently deploy deep neural networks (DNNs) on devices that limited computation resources and tight power budgets, such as mobile and IoT (Internet of Things) devices. Consequently, model compression is one of the most critical topics in modern deep learning. Typically, the state-of-the-art model compression methods suffer from a big limitation: they are only based on heuristics rather than theoretical foundation and thus offer no worst-case guarantees. To bridge this gap, Baykal et. al. [2018a] suggested using a coreset, a small weighted subset of the data that provably approximates the original data set, to sparsify the parameters of a trained fully-connected neural network by sampling a number of neural network parameters based on the importance of the data. However, the sampling procedure is data-dependent and can only be only be performed after an expensive training phase. We propose the use of data-independent coresets to perform provable model compression without the need for training. We first prove that there exists a coreset whose size is independent of the input size of the data for any neuron whose activation function is from a family of functions that includes variants of ReLU, sigmoid and others. We then provide a compression-based algorithm that constructs these coresets and explicitly applies neuron pruning for the underlying model. We demonstrate the effectiveness of our methods with experimental evaluations for both synthetic and real-world benchmark network compression. In particular, our framework provides up to 90% compression on the LeNet-300-100 architecture on MNIST and actually improves the accuracy.