Multiaccuracy and Multicalibration via Proxy Groups

As the use of predictive machine learning algorithms increases in high-stakes decision-making, it is imperative that these algorithms are fair across sensitive groups. Unfortunately, measuring and enforcing fairness in real-world applications can be challenging due to missing or incomplete sensitive group data. Proxy-sensitive attributes have been proposed as a practical and effective solution in these settings, but only for parity-based fairness notions. Knowing how to evaluate and control for fairness with missing sensitive group data for newer and more flexible frameworks, such as multiaccuracy and multicalibration, remains unexplored. In this work, we address this gap by demonstrating that in the absence of sensitive group data, proxy-sensitive attributes can provably be used to derive actionable upper bounds on the true multiaccuracy and multicalibration, providing insights into a model's potential worst-case fairness violations. Additionally, we show that adjusting models to satisfy multiaccuracy and multicalibration across proxy-sensitive attributes can significantly mitigate these violations for the true, but unknown, sensitive groups. Through several experiments on real-world datasets, we illustrate that approximate multiaccuracy and multicalibration can be achieved even when sensitive group information is incomplete or unavailable.

Sufficient and Necessary Explanations (and What Lies in Between)

As complex machine learning models continue to find applications in high-stakes decision-making scenarios, it is crucial that we can explain and understand their predictions. Post-hoc explanation methods provide useful insights by identifying important features in an input $\mathbf{x}$ with respect to the model output $f(\mathbf{x})$. In this work, we formalize and study two precise notions of feature importance for general machine learning models: sufficiency and necessity. We demonstrate how these two types of explanations, albeit intuitive and simple, can fall short in providing a complete picture of which features a model finds important. To this end, we propose a unified notion of importance that circumvents these limitations by exploring a continuum along a necessity-sufficiency axis. Our unified notion, we show, has strong ties to other popular definitions of feature importance, like those based on conditional independence and game-theoretic quantities like Shapley values. Crucially, we demonstrate how a unified perspective allows us to detect important features that could be missed by either of the previous approaches alone.

Estimating and Controlling for Fairness via Sensitive Attribute Predictors

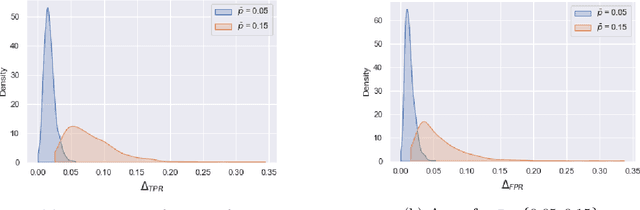
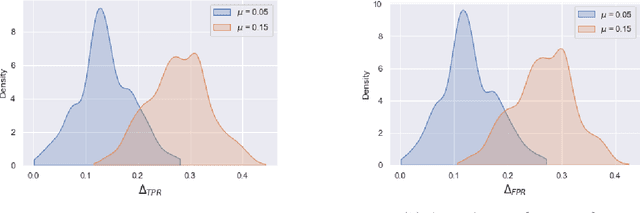
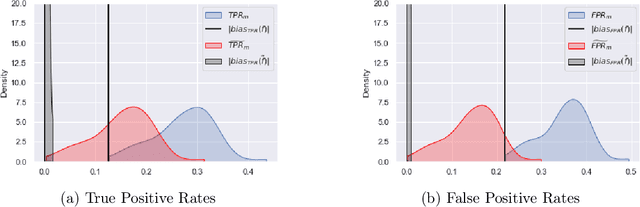
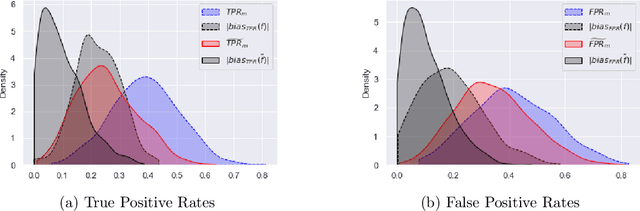
Although machine learning classifiers have been increasingly used in high-stakes decision making (e.g., cancer diagnosis, criminal prosecution decisions), they have demonstrated biases against underrepresented groups. Standard definitions of fairness require access to sensitive attributes of interest (e.g., gender and race), which are often unavailable. In this work we demonstrate that in these settings where sensitive attributes are unknown, one can still reliably estimate and ultimately control for fairness by using proxy sensitive attributes derived from a sensitive attribute predictor. Specifically, we first show that with just a little knowledge of the complete data distribution, one may use a sensitive attribute predictor to obtain upper and lower bounds of the classifier's true fairness metric. Second, we demonstrate how one can provably control for fairness with respect to the true sensitive attributes by controlling for fairness with respect to the proxy sensitive attributes. Our results hold under assumptions that are significantly milder than previous works. We illustrate our results on a series of synthetic and real datasets.

From Shapley back to Pearson: Hypothesis Testing via the Shapley Value

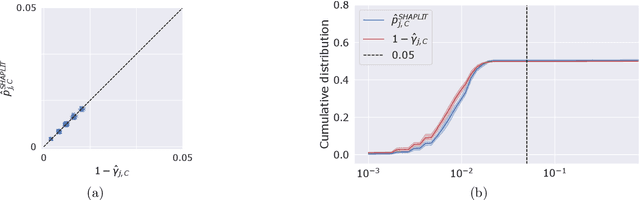
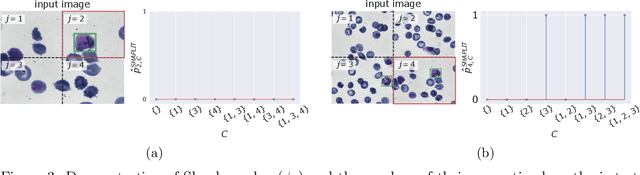
Machine learning models, in particular artificial neural networks, are increasingly used to inform decision making in high-stakes scenarios across a variety of fields--from financial services, to public safety, and healthcare. While neural networks have achieved remarkable performance in many settings, their complex nature raises concerns on their reliability, trustworthiness, and fairness in real-world scenarios. As a result, several a-posteriori explanation methods have been proposed to highlight the features that influence a model's prediction. Notably, the Shapley value--a game theoretic quantity that satisfies several desirable properties--has gained popularity in the machine learning explainability literature. More traditionally, however, feature importance in statistical learning has been formalized by conditional independence, and a standard way to test for it is via Conditional Randomization Tests (CRTs). So far, these two perspectives on interpretability and feature importance have been considered distinct and separate. In this work, we show that Shapley-based explanation methods and conditional independence testing for feature importance are closely related. More precisely, we prove that evaluating a Shapley coefficient amounts to performing a specific set of conditional independence tests, as implemented by a procedure similar to the CRT but for a different null hypothesis. Furthermore, the obtained game-theoretic values upper bound the $p$-values of such tests. As a result, we grant large Shapley coefficients with a precise statistical sense of importance with controlled type I error.