Sufficient and Necessary Explanations (and What Lies in Between)

As complex machine learning models continue to find applications in high-stakes decision-making scenarios, it is crucial that we can explain and understand their predictions. Post-hoc explanation methods provide useful insights by identifying important features in an input $\mathbf{x}$ with respect to the model output $f(\mathbf{x})$. In this work, we formalize and study two precise notions of feature importance for general machine learning models: sufficiency and necessity. We demonstrate how these two types of explanations, albeit intuitive and simple, can fall short in providing a complete picture of which features a model finds important. To this end, we propose a unified notion of importance that circumvents these limitations by exploring a continuum along a necessity-sufficiency axis. Our unified notion, we show, has strong ties to other popular definitions of feature importance, like those based on conditional independence and game-theoretic quantities like Shapley values. Crucially, we demonstrate how a unified perspective allows us to detect important features that could be missed by either of the previous approaches alone.

Estimating and Controlling for Fairness via Sensitive Attribute Predictors

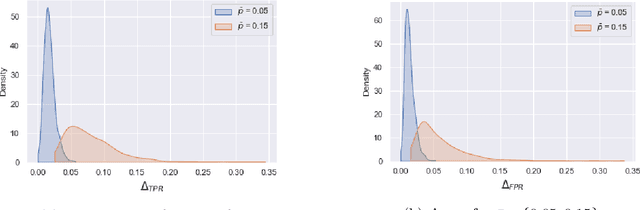
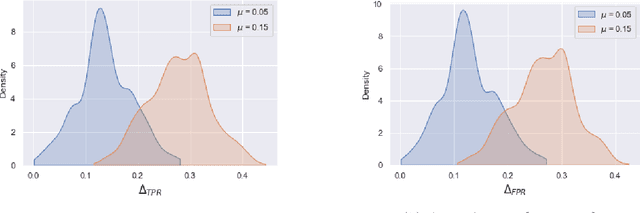
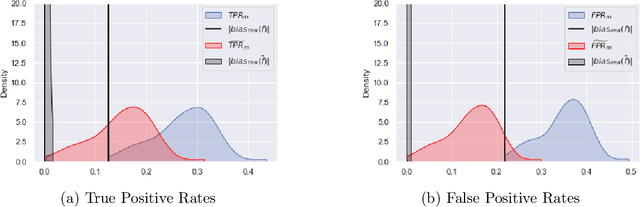
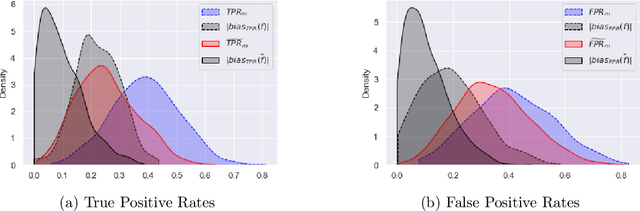
Although machine learning classifiers have been increasingly used in high-stakes decision making (e.g., cancer diagnosis, criminal prosecution decisions), they have demonstrated biases against underrepresented groups. Standard definitions of fairness require access to sensitive attributes of interest (e.g., gender and race), which are often unavailable. In this work we demonstrate that in these settings where sensitive attributes are unknown, one can still reliably estimate and ultimately control for fairness by using proxy sensitive attributes derived from a sensitive attribute predictor. Specifically, we first show that with just a little knowledge of the complete data distribution, one may use a sensitive attribute predictor to obtain upper and lower bounds of the classifier's true fairness metric. Second, we demonstrate how one can provably control for fairness with respect to the true sensitive attributes by controlling for fairness with respect to the proxy sensitive attributes. Our results hold under assumptions that are significantly milder than previous works. We illustrate our results on a series of synthetic and real datasets.