Going beyond explainability in multi-modal stroke outcome prediction models

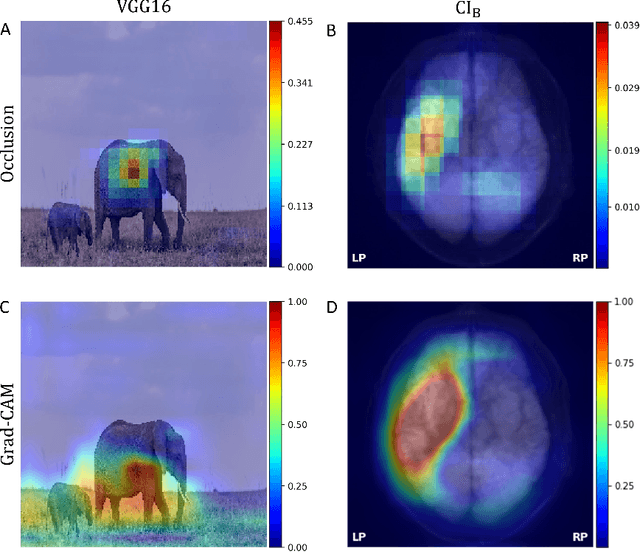
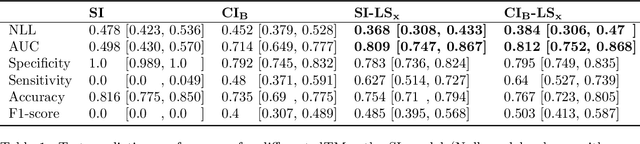
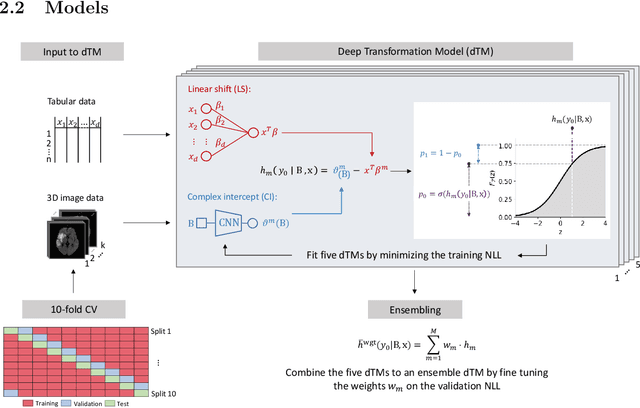
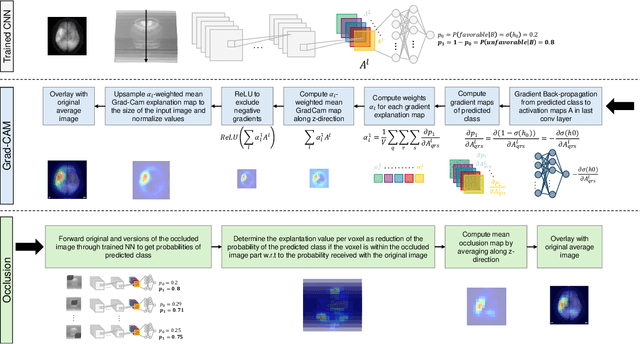
Aim: This study aims to enhance interpretability and explainability of multi-modal prediction models integrating imaging and tabular patient data. Methods: We adapt the xAI methods Grad-CAM and Occlusion to multi-modal, partly interpretable deep transformation models (dTMs). DTMs combine statistical and deep learning approaches to simultaneously achieve state-of-the-art prediction performance and interpretable parameter estimates, such as odds ratios for tabular features. Based on brain imaging and tabular data from 407 stroke patients, we trained dTMs to predict functional outcome three months after stroke. We evaluated the models using different discriminatory metrics. The adapted xAI methods were used to generated explanation maps for identification of relevant image features and error analysis. Results: The dTMs achieve state-of-the-art prediction performance, with area under the curve (AUC) values close to 0.8. The most important tabular predictors of functional outcome are functional independence before stroke and NIHSS on admission, a neurological score indicating stroke severity. Explanation maps calculated from brain imaging dTMs for functional outcome highlighted critical brain regions such as the frontal lobe, which is known to be linked to age which in turn increases the risk for unfavorable outcomes. Similarity plots of the explanation maps revealed distinct patterns which give insight into stroke pathophysiology, support developing novel predictors of stroke outcome and enable to identify false predictions. Conclusion: By adapting methods for explanation maps to dTMs, we enhanced the explainability of multi-modal and partly interpretable prediction models. The resulting explanation maps facilitate error analysis and support hypothesis generation regarding the significance of specific image regions in outcome prediction.

Interpretable Neural Causal Models with TRAM-DAGs

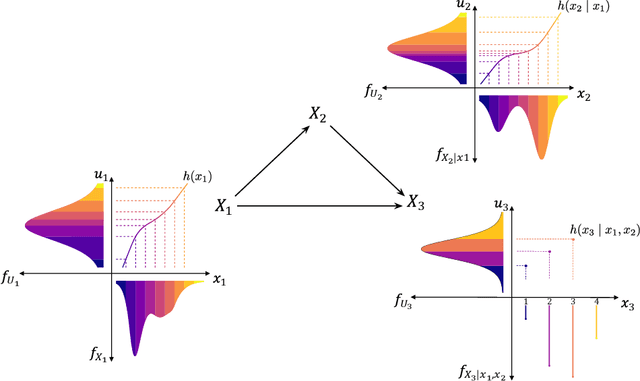
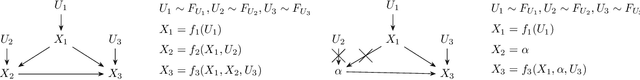
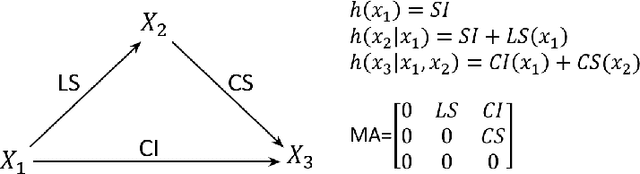
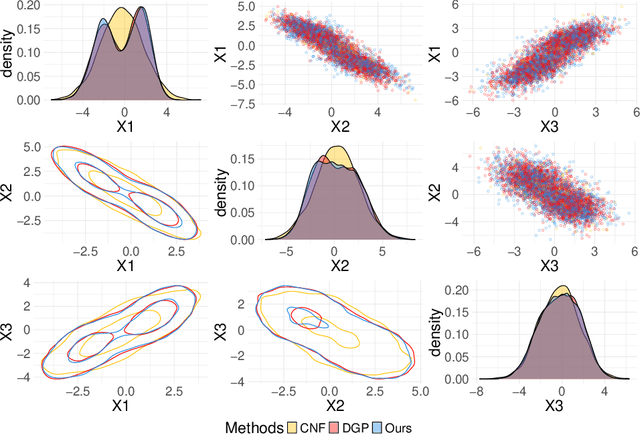
The ultimate goal of most scientific studies is to understand the underlying causal mechanism between the involved variables. Structural causal models (SCMs) are widely used to represent such causal mechanisms. Given an SCM, causal queries on all three levels of Pearl's causal hierarchy can be answered: $L_1$ observational, $L_2$ interventional, and $L_3$ counterfactual. An essential aspect of modeling the SCM is to model the dependency of each variable on its causal parents. Traditionally this is done by parametric statistical models, such as linear or logistic regression models. This allows to handle all kinds of data types and fit interpretable models but bears the risk of introducing a bias. More recently neural causal models came up using neural networks (NNs) to model the causal relationships, allowing the estimation of nearly any underlying functional form without bias. However, current neural causal models are generally restricted to continuous variables and do not yield an interpretable form of the causal relationships. Transformation models range from simple statistical regressions to complex networks and can handle continuous, ordinal, and binary data. Here, we propose to use TRAMs to model the functional relationships in SCMs allowing us to bridge the gap between interpretability and flexibility in causal modeling. We call this method TRAM-DAG and assume currently that the underlying directed acyclic graph is known. For the fully observed case, we benchmark TRAM-DAGs against state-of-the-art statistical and NN-based causal models. We show that TRAM-DAGs are interpretable but also achieve equal or superior performance in queries ranging from $L_1$ to $L_3$ in the causal hierarchy. For the continuous case, TRAM-DAGs allow for counterfactual queries for three common causal structures, including unobserved confounding.

Bayesian Semi-structured Subspace Inference

Semi-structured regression models enable the joint modeling of interpretable structured and complex unstructured feature effects. The structured model part is inspired by statistical models and can be used to infer the input-output relationship for features of particular importance. The complex unstructured part defines an arbitrary deep neural network and thereby provides enough flexibility to achieve competitive prediction performance. While these models can also account for aleatoric uncertainty, there is still a lack of work on accounting for epistemic uncertainty. In this paper, we address this problem by presenting a Bayesian approximation for semi-structured regression models using subspace inference. To this end, we extend subspace inference for joint posterior sampling from a full parameter space for structured effects and a subspace for unstructured effects. Apart from this hybrid sampling scheme, our method allows for tunable complexity of the subspace and can capture multiple minima in the loss landscape. Numerical experiments validate our approach's efficacy in recovering structured effect parameter posteriors in semi-structured models and approaching the full-space posterior distribution of MCMC for increasing subspace dimension. Further, our approach exhibits competitive predictive performance across simulated and real-world datasets.

Single-shot Bayesian approximation for neural networks

Deep neural networks (NNs) are known for their high-prediction performances. However, NNs are prone to yield unreliable predictions when encountering completely new situations without indicating their uncertainty. Bayesian variants of NNs (BNNs), such as Monte Carlo (MC) dropout BNNs, do provide uncertainty measures and simultaneously increase the prediction performance. The only disadvantage of BNNs is their higher computation time during test time because they rely on a sampling approach. Here we present a single-shot MC dropout approximation that preserves the advantages of BNNs while being as fast as NNs. Our approach is based on moment propagation (MP) and allows to analytically approximate the expected value and the variance of the MC dropout signal for commonly used layers in NNs, i.e. convolution, max pooling, dense, softmax, and dropout layers. The MP approach can convert an NN into a BNN without re-training given the NN has been trained with standard dropout. We evaluate our approach on different benchmark datasets and a simulated toy example in a classification and regression setting. We demonstrate that our single-shot MC dropout approximation resembles the point estimate and the uncertainty estimate of the predictive distribution that is achieved with an MC approach, while being fast enough for real-time deployments of BNNs. We show that using part of the saved time to combine our MP approach with deep ensemble techniques does further improve the uncertainty measures.

Deep interpretable ensembles

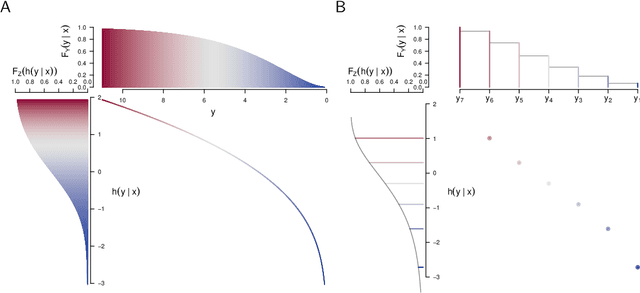
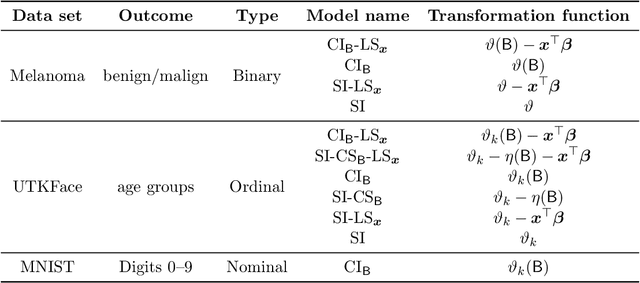
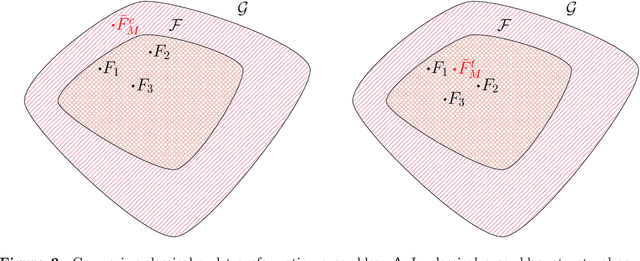
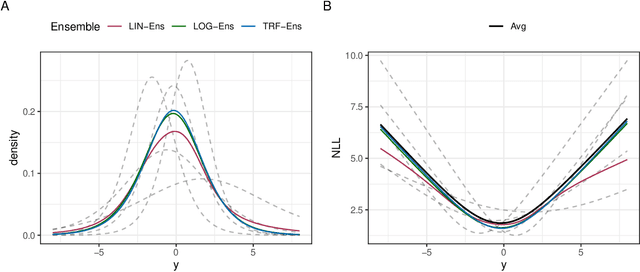
Ensembles improve prediction performance and allow uncertainty quantification by aggregating predictions from multiple models. In deep ensembling, the individual models are usually black box neural networks, or recently, partially interpretable semi-structured deep transformation models. However, interpretability of the ensemble members is generally lost upon aggregation. This is a crucial drawback of deep ensembles in high-stake decision fields, in which interpretable models are desired. We propose a novel transformation ensemble which aggregates probabilistic predictions with the guarantee to preserve interpretability and yield uniformly better predictions than the ensemble members on average. Transformation ensembles are tailored towards interpretable deep transformation models but are applicable to a wider range of probabilistic neural networks. In experiments on several publicly available data sets, we demonstrate that transformation ensembles perform on par with classical deep ensembles in terms of prediction performance, discrimination, and calibration. In addition, we demonstrate how transformation ensembles quantify both aleatoric and epistemic uncertainty, and produce minimax optimal predictions under certain conditions.

Short-Term Density Forecasting of Low-Voltage Load using Bernstein-Polynomial Normalizing Flows

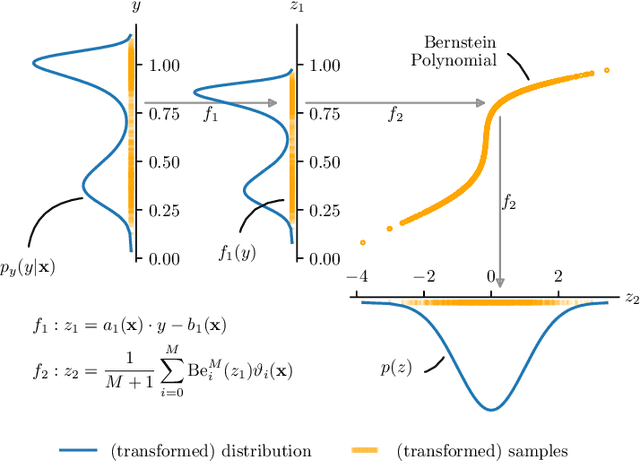
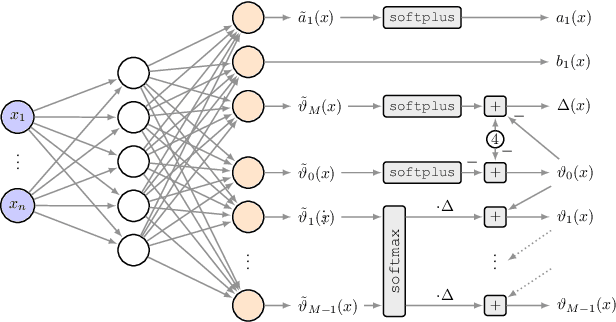
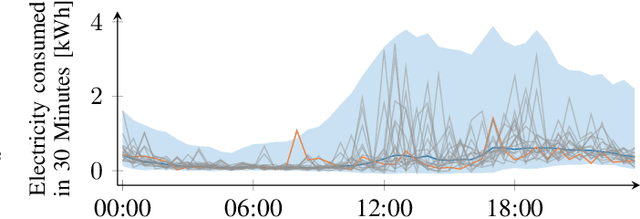
The transition to a fully renewable energy grid requires better forecasting of demand at the low-voltage level to increase efficiency and ensure reliable control. However, high fluctuations and increasing electrification cause huge forecast variability, not reflected in traditional point estimates. Probabilistic load forecasts take future uncertainties into account and thus allow more informed decision-making for the planning and operation of low-carbon energy systems. We propose an approach for flexible conditional density forecasting of short-term load based on Bernstein polynomial normalizing flows, where a neural network controls the parameters of the flow. In an empirical study with 363 smart meter customers, our density predictions compare favorably against Gaussian and Gaussian mixture densities. Also, they outperform a non-parametric approach based on the pinball loss for 24h-ahead load forecasting for two different neural network architectures.

Bernstein Flows for Flexible Posteriors in Variational Bayes

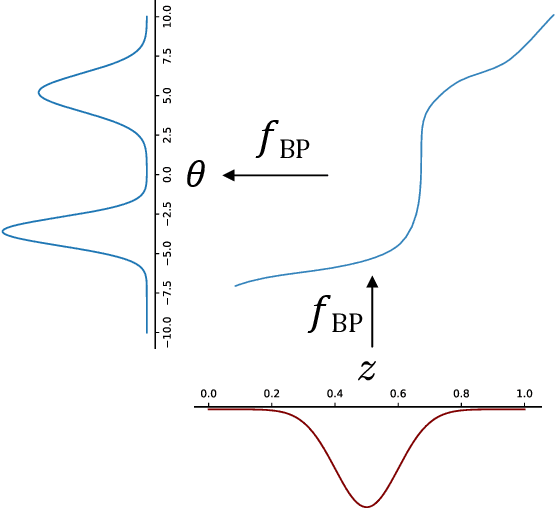
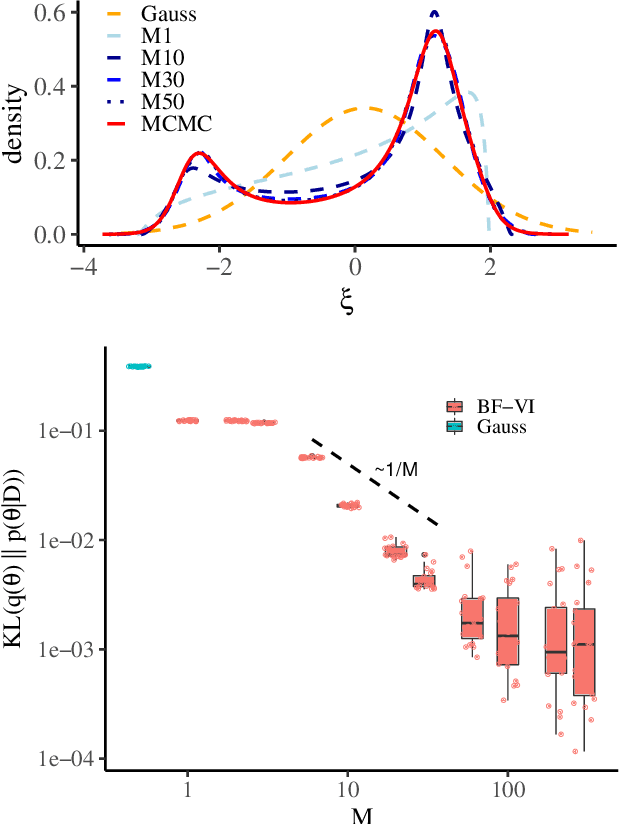
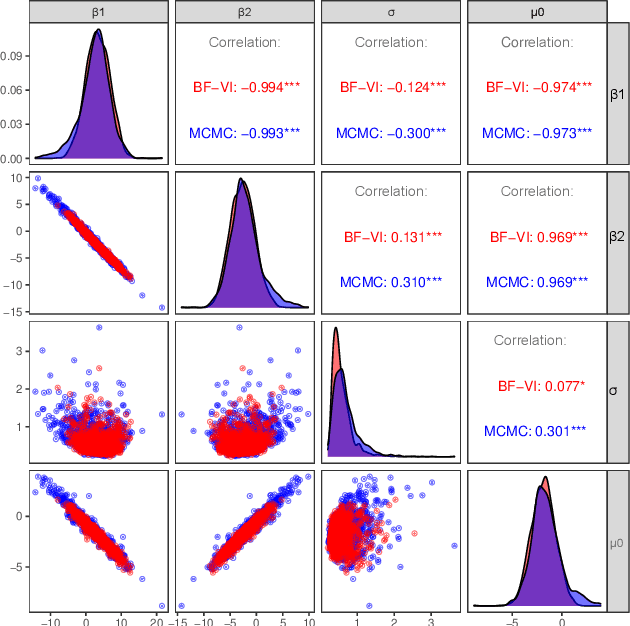
Variational inference (VI) is a technique to approximate difficult to compute posteriors by optimization. In contrast to MCMC, VI scales to many observations. In the case of complex posteriors, however, state-of-the-art VI approaches often yield unsatisfactory posterior approximations. This paper presents Bernstein flow variational inference (BF-VI), a robust and easy-to-use method, flexible enough to approximate complex multivariate posteriors. BF-VI combines ideas from normalizing flows and Bernstein polynomial-based transformation models. In benchmark experiments, we compare BF-VI solutions with exact posteriors, MCMC solutions, and state-of-the-art VI methods including normalizing flow based VI. We show for low-dimensional models that BF-VI accurately approximates the true posterior; in higher-dimensional models, BF-VI outperforms other VI methods. Further, we develop with BF-VI a Bayesian model for the semi-structured Melanoma challenge data, combining a CNN model part for image data with an interpretable model part for tabular data, and demonstrate for the first time how the use of VI in semi-structured models.

Transformation Models for Flexible Posteriors in Variational Bayes

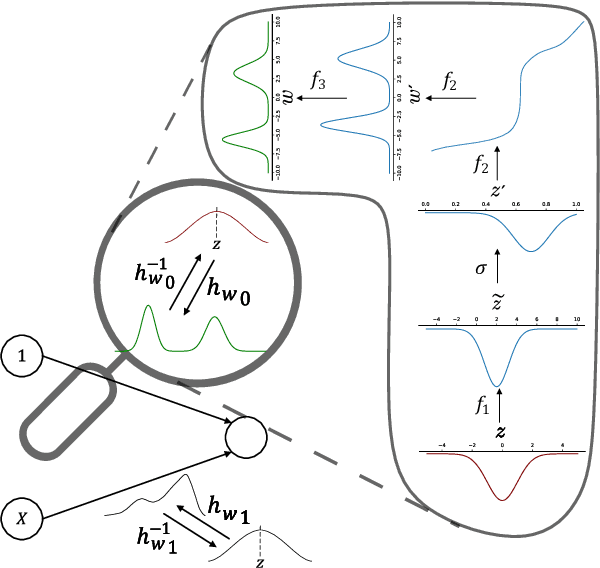
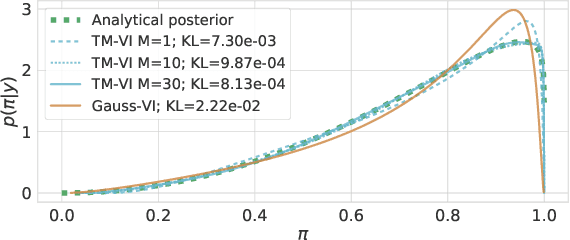
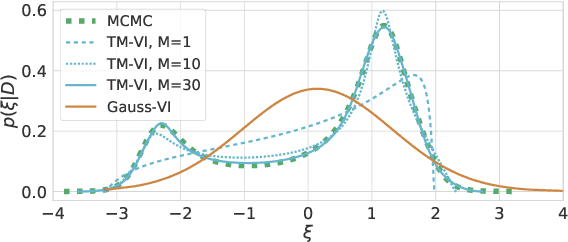
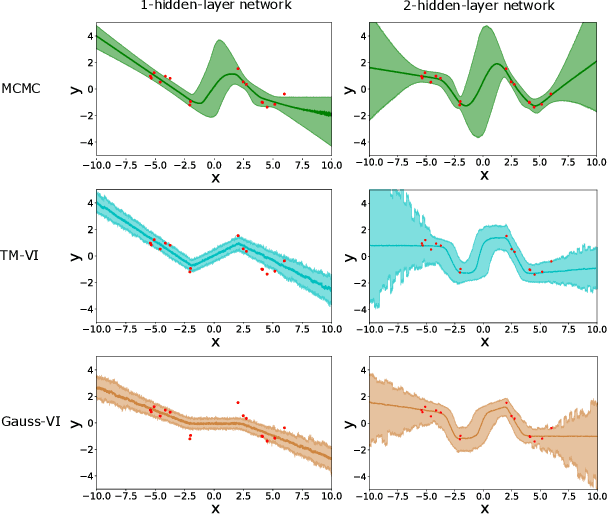
The main challenge in Bayesian models is to determine the posterior for the model parameters. Already, in models with only one or few parameters, the analytical posterior can only be determined in special settings. In Bayesian neural networks, variational inference is widely used to approximate difficult-to-compute posteriors by variational distributions. Usually, Gaussians are used as variational distributions (Gaussian-VI) which limits the quality of the approximation due to their limited flexibility. Transformation models on the other hand are flexible enough to fit any distribution. Here we present transformation model-based variational inference (TM-VI) and demonstrate that it allows to accurately approximate complex posteriors in models with one parameter and also works in a mean-field fashion for multi-parameter models like neural networks.

Ordinal Neural Network Transformation Models: Deep and interpretable regression models for ordinal outcomes

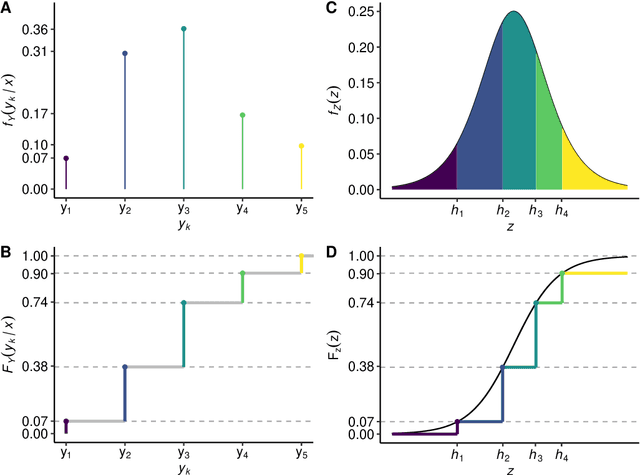
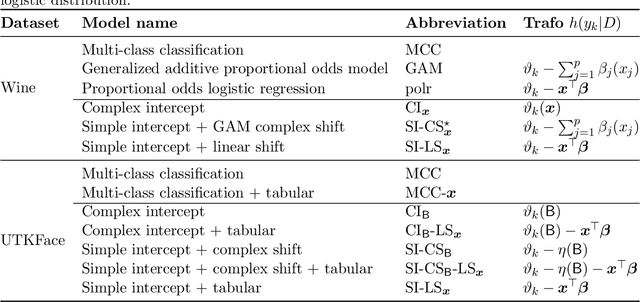
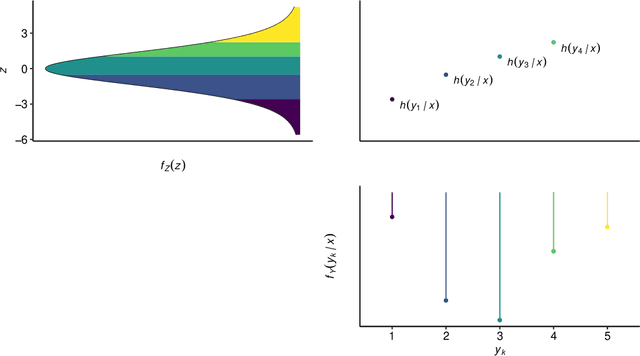
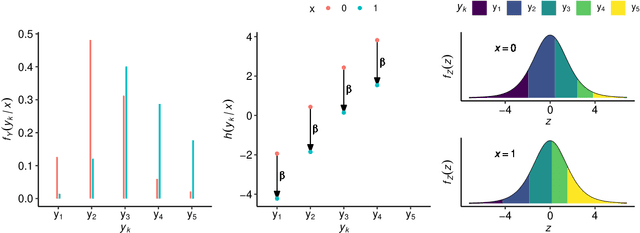
Outcomes with a natural order commonly occur in prediction tasks and oftentimes the available input data are a mixture of complex data, like images, and tabular predictors. Although deep Learning (DL) methods have shown outstanding performance on image classification, most models treat ordered outcomes as unordered and lack interpretability. In contrast, classical ordinal regression models yield interpretable predictor effects but are limited to tabular input data. Here, we present the highly modular class of ordinal neural network transformation models (ONTRAMs). Transformation models use a parametric transformation function and a simple distribution to trade off flexibility and interpretability of individual model components. In ONTRAMs, this trade-off is achieved by additively decomposing the transformation function into terms for the tabular and image data using a set of jointly trained neural networks. We show that the most flexible ONTRAMs achieve on-par performance with DL classifiers while outperforming them in training speed. We discuss how to interpret components of ONTRAMs in general and in the case of correlated tabular and image data. Taken together, ONTRAMs join benefits of DL and distributional regression to create interpretable prediction models for ordinal outcomes.

Integrating uncertainty in deep neural networks for MRI based stroke analysis

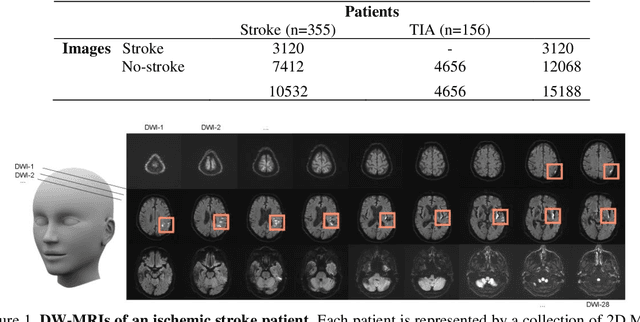
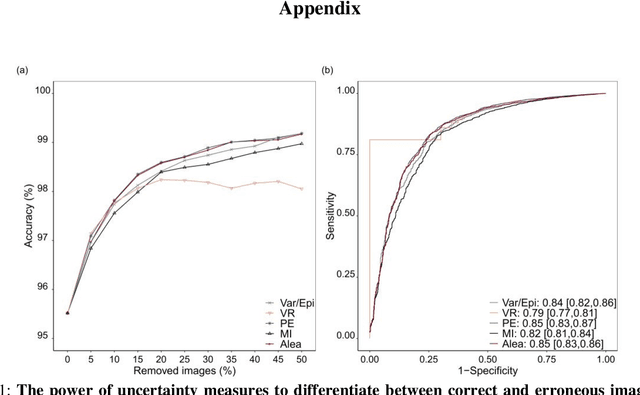
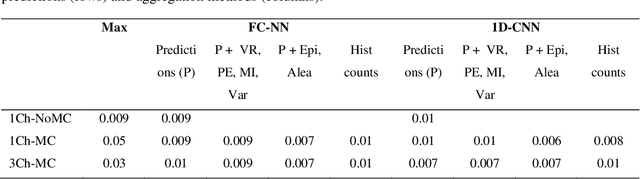
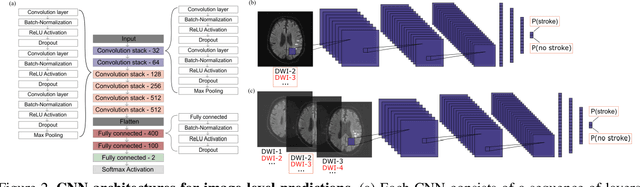
At present, the majority of the proposed Deep Learning (DL) methods provide point predictions without quantifying the models uncertainty. However, a quantification of the reliability of automated image analysis is essential, in particular in medicine when physicians rely on the results for making critical treatment decisions. In this work, we provide an entire framework to diagnose ischemic stroke patients incorporating Bayesian uncertainty into the analysis procedure. We present a Bayesian Convolutional Neural Network (CNN) yielding a probability for a stroke lesion on 2D Magnetic Resonance (MR) images with corresponding uncertainty information about the reliability of the prediction. For patient-level diagnoses, different aggregation methods are proposed and evaluated, which combine the single image-level predictions. Those methods take advantage of the uncertainty in image predictions and report model uncertainty at the patient-level. In a cohort of 511 patients, our Bayesian CNN achieved an accuracy of 95.33% at the image-level representing a significant improvement of 2% over a non-Bayesian counterpart. The best patient aggregation method yielded 95.89% of accuracy. Integrating uncertainty information about image predictions in aggregation models resulted in higher uncertainty measures to false patient classifications, which enabled to filter critical patient diagnoses that are supposed to be closer examined by a medical doctor. We therefore recommend using Bayesian approaches not only for improved image-level prediction and uncertainty estimation but also for the detection of uncertain aggregations at the patient-level.