Utility-Fairness Trade-Offs and How to Find Them

When building classification systems with demographic fairness considerations, there are two objectives to satisfy: 1) maximizing utility for the specific task and 2) ensuring fairness w.r.t. a known demographic attribute. These objectives often compete, so optimizing both can lead to a trade-off between utility and fairness. While existing works acknowledge the trade-offs and study their limits, two questions remain unanswered: 1) What are the optimal trade-offs between utility and fairness? and 2) How can we numerically quantify these trade-offs from data for a desired prediction task and demographic attribute of interest? This paper addresses these questions. We introduce two utility-fairness trade-offs: the Data-Space and Label-Space Trade-off. The trade-offs reveal three regions within the utility-fairness plane, delineating what is fully and partially possible and impossible. We propose U-FaTE, a method to numerically quantify the trade-offs for a given prediction task and group fairness definition from data samples. Based on the trade-offs, we introduce a new scheme for evaluating representations. An extensive evaluation of fair representation learning methods and representations from over 1000 pre-trained models revealed that most current approaches are far from the estimated and achievable fairness-utility trade-offs across multiple datasets and prediction tasks.

Adversarial Representation Learning With Closed-Form Solvers

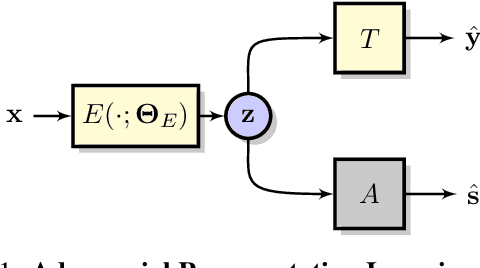
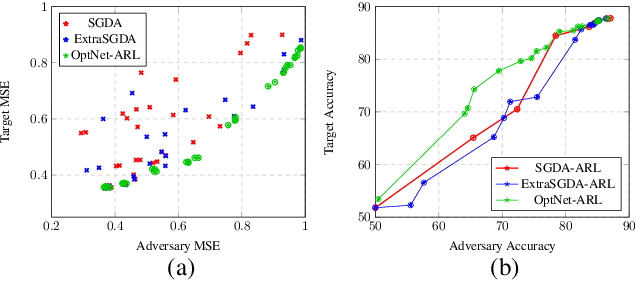
Adversarial representation learning aims to learn data representations for a target task while removing unwanted sensitive information at the same time. Existing methods learn model parameters iteratively through stochastic gradient descent-ascent, which is often unstable and unreliable in practice. To overcome this challenge, we adopt closed-form solvers for the adversary and target task. We model them as kernel ridge regressors and analytically determine an upper-bound on the optimal dimensionality of representation. Our solution, dubbed OptNet-ARL, reduces to a stable one one-shot optimization problem that can be solved reliably and efficiently. OptNet-ARL can be easily generalized to the case of multiple target tasks and sensitive attributes. Numerical experiments, on both small and large scale datasets, show that, from an optimization perspective, OptNet-ARL is stable and exhibits three to five times faster convergence. Performance wise, when the target and sensitive attributes are dependent, OptNet-ARL learns representations that offer a better trade-off front between (a) utility and bias for fair classification and (b) utility and privacy by mitigating leakage of private information than existing solutions.

On the Fundamental Trade-offs in Learning Invariant Representations

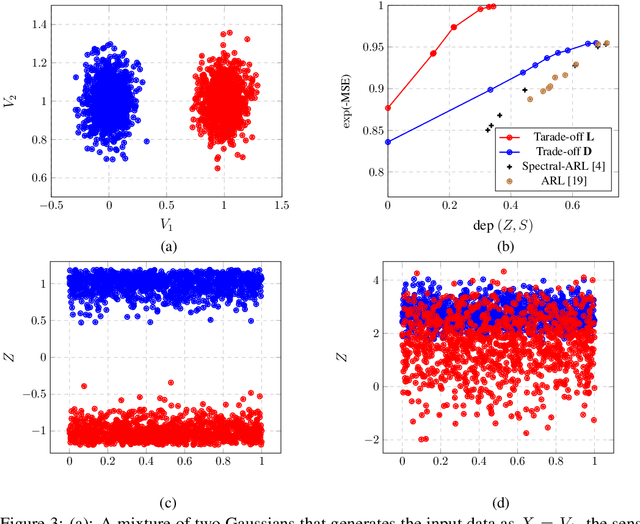
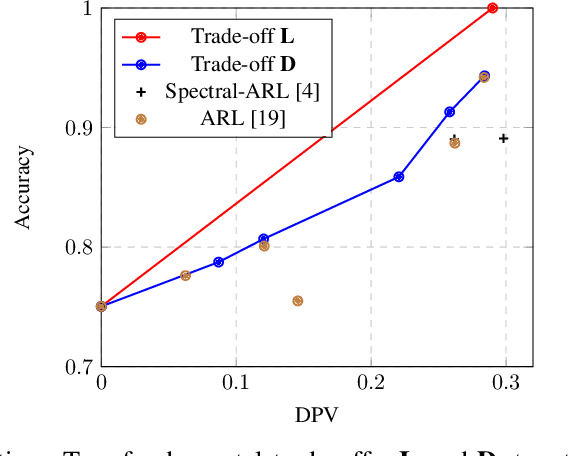
Many applications of representation learning, such as privacy-preservation, algorithmic fairness and domain adaptation, desire explicit control over semantic information being discarded. This goal is often formulated as satisfying two potentially competing objectives: maximizing utility for predicting a target attribute while simultaneously being independent or invariant with respect to a known semantic attribute. In this paper, we \emph{identify and determine} two fundamental trade-offs between utility and semantic dependence induced by the statistical dependencies between the data and its corresponding target and semantic attributes. We derive closed-form solutions for the global optima of the underlying optimization problems under mild assumptions, which in turn yields closed formulae for the exact trade-offs. We also derive empirical estimates of the trade-offs and show their convergence to the corresponding population counterparts. Finally, we numerically quantify the trade-offs on representative problems and compare to the solutions achieved by baseline representation learning algorithms.

On the Global Optima of Kernelized Adversarial Representation Learning

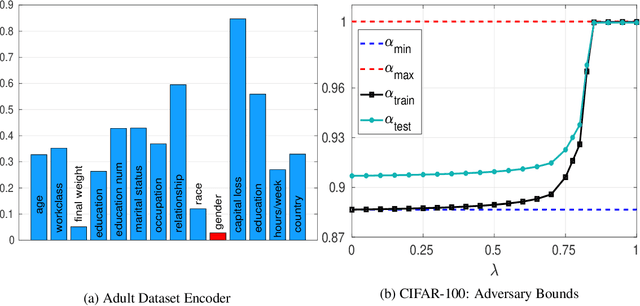
Adversarial representation learning is a promising paradigm for obtaining data representations that are invariant to certain sensitive attributes while retaining the information necessary for predicting target attributes. Existing approaches solve this problem through iterative adversarial minimax optimization and lack theoretical guarantees. In this paper, we first study the "linear" form of this problem i.e., the setting where all the players are linear functions. We show that the resulting optimization problem is both non-convex and non-differentiable. We obtain an exact closed-form expression for its global optima through spectral learning and provide performance guarantees in terms of analytical bounds on the achievable utility and invariance. We then extend this solution and analysis to non-linear functions through kernel representation. Numerical experiments on UCI, Extended Yale B and CIFAR-100 datasets indicate that, (a) practically, our solution is ideal for "imparting" provable invariance to any biased pre-trained data representation, and (b) empirically, the trade-off between utility and invariance provided by our solution is comparable to iterative minimax optimization of existing deep neural network based approaches. Code is available at https://github.com/human-analysis/Kernel-ARL