On the Fundamental Trade-offs in Learning Invariant Representations

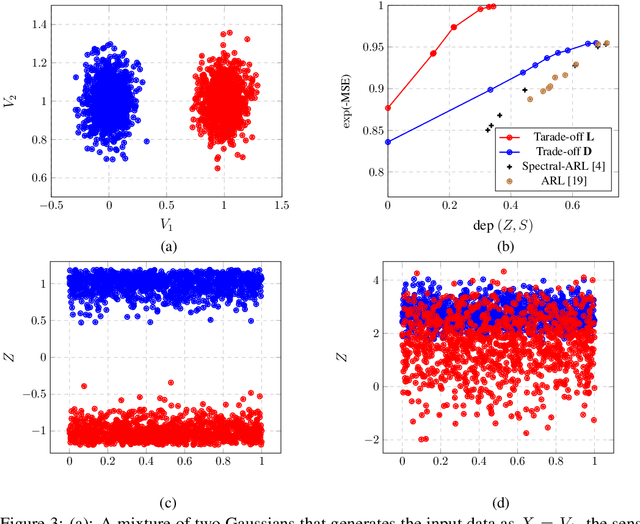
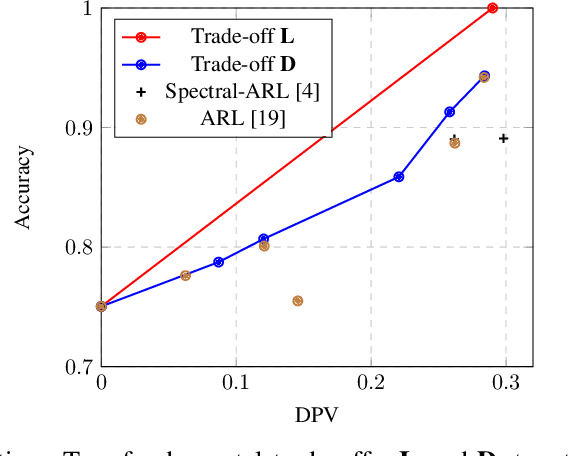
Many applications of representation learning, such as privacy-preservation, algorithmic fairness and domain adaptation, desire explicit control over semantic information being discarded. This goal is often formulated as satisfying two potentially competing objectives: maximizing utility for predicting a target attribute while simultaneously being independent or invariant with respect to a known semantic attribute. In this paper, we \emph{identify and determine} two fundamental trade-offs between utility and semantic dependence induced by the statistical dependencies between the data and its corresponding target and semantic attributes. We derive closed-form solutions for the global optima of the underlying optimization problems under mild assumptions, which in turn yields closed formulae for the exact trade-offs. We also derive empirical estimates of the trade-offs and show their convergence to the corresponding population counterparts. Finally, we numerically quantify the trade-offs on representative problems and compare to the solutions achieved by baseline representation learning algorithms.