Deep Matrix Factorization with Adaptive Weights for Multi-View Clustering

Recently, deep matrix factorization has been established as a powerful model for unsupervised tasks, achieving promising results, especially for multi-view clustering. However, existing methods often lack effective feature selection mechanisms and rely on empirical hyperparameter selection. To address these issues, we introduce a novel Deep Matrix Factorization with Adaptive Weights for Multi-View Clustering (DMFAW). Our method simultaneously incorporates feature selection and generates local partitions, enhancing clustering results. Notably, the features weights are controlled and adjusted by a parameter that is dynamically updated using Control Theory inspired mechanism, which not only improves the model's stability and adaptability to diverse datasets but also accelerates convergence. A late fusion approach is then proposed to align the weighted local partitions with the consensus partition. Finally, the optimization problem is solved via an alternating optimization algorithm with theoretically guaranteed convergence. Extensive experiments on benchmark datasets highlight that DMFAW outperforms state-of-the-art methods in terms of clustering performance.

CADMR: Cross-Attention and Disentangled Learning for Multimodal Recommender Systems

The increasing availability and diversity of multimodal data in recommender systems offer new avenues for enhancing recommendation accuracy and user satisfaction. However, these systems must contend with high-dimensional, sparse user-item rating matrices, where reconstructing the matrix with only small subsets of preferred items for each user poses a significant challenge. To address this, we propose CADMR, a novel autoencoder-based multimodal recommender system framework. CADMR leverages multi-head cross-attention mechanisms and Disentangled Learning to effectively integrate and utilize heterogeneous multimodal data in reconstructing the rating matrix. Our approach first disentangles modality-specific features while preserving their interdependence, thereby learning a joint latent representation. The multi-head cross-attention mechanism is then applied to enhance user-item interaction representations with respect to the learned multimodal item latent representations. We evaluate CADMR on three benchmark datasets, demonstrating significant performance improvements over state-of-the-art methods.

Multi-modal Multi-view Clustering based on Non-negative Matrix Factorization

By combining related objects, unsupervised machine learning techniques aim to reveal the underlying patterns in a data set. Non-negative Matrix Factorization (NMF) is a data mining technique that splits data matrices by imposing restrictions on the elements' non-negativity into two matrices: one representing the data partitions and the other to represent the cluster prototypes of the data set. This method has attracted a lot of attention and is used in a wide range of applications, including text mining, clustering, language modeling, music transcription, and neuroscience (gene separation). The interpretation of the generated matrices is made simpler by the absence of negative values. In this article, we propose a study on multi-modal clustering algorithms and present a novel method called multi-modal multi-view non-negative matrix factorization, in which we analyze the collaboration of several local NMF models. The experimental results show the value of the proposed approach, which was evaluated using a variety of data sets, and the obtained results are very promising compared to state of art methods.

A quantum learning approach based on Hidden Markov Models for failure scenarios generation

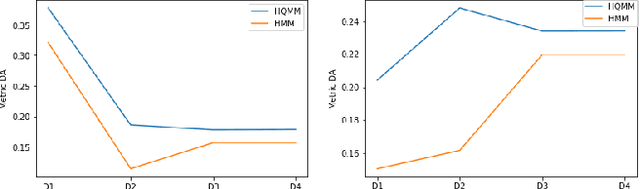
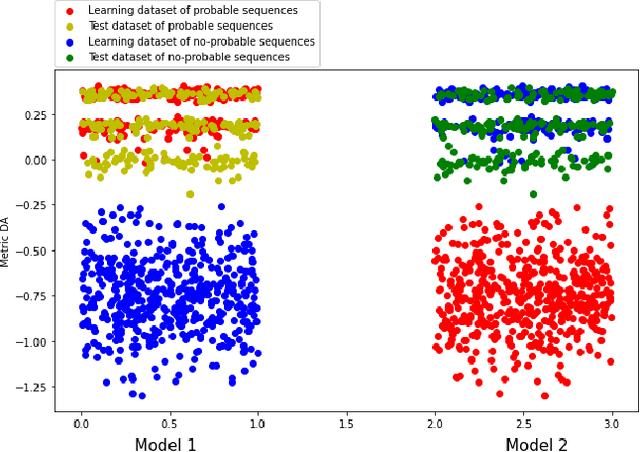
Finding the failure scenarios of a system is a very complex problem in the field of Probabilistic Safety Assessment (PSA). In order to solve this problem we will use the Hidden Quantum Markov Models (HQMMs) to create a generative model. Therefore, in this paper, we will study and compare the results of HQMMs and classical Hidden Markov Models HMM on a real datasets generated from real small systems in the field of PSA. As a quality metric we will use Description accuracy DA and we will show that the quantum approach gives better results compared with the classical approach, and we will give a strategy to identify the probable and no-probable failure scenarios of a system.

Convex Non-negative Matrix Factorization Through Quantum Annealing

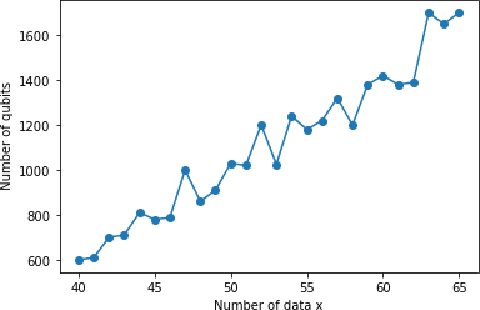
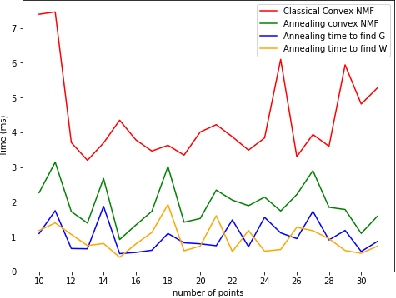
In this paper we provide the quantum version of the Convex Non-negative Matrix Factorization algorithm (Convex-NMF) by using the D-wave quantum annealer. More precisely, we use D-wave 2000Q to find the low rank approximation of a fixed real-valued matrix X by the product of two non-negative matrices factors W and G such that the Frobenius norm of the difference X-XWG is minimized. In order to solve this optimization problem we proceed in two steps. In the first step we transform the global real optimization problem depending on W,G into two quadratic unconstrained binary optimization problems (QUBO) depending on W and G respectively. In the second step we use an alternative strategy between the two QUBO problems corresponding to W and G to find the global solution. The running of these two QUBO problems on D-wave 2000Q need to use an embedding to the chimera graph of D-wave 2000Q, this embedding is limited by the number of qubits of D-wave 2000Q. We perform a study on the maximum number of real data to be used by our approach on D-wave 2000Q. The proposed study is based on the number of qubits used to represent each real variable. We also tested our approach on D-Wave 2000Q with several randomly generated data sets to prove that our approach is faster than the classical approach and also to prove that it gets the best results.

Co-clustering through Optimal Transport

In this paper, we present a novel method for co-clustering, an unsupervised learning approach that aims at discovering homogeneous groups of data instances and features by grouping them simultaneously. The proposed method uses the entropy regularized optimal transport between empirical measures defined on data instances and features in order to obtain an estimated joint probability density function represented by the optimal coupling matrix. This matrix is further factorized to obtain the induced row and columns partitions using multiscale representations approach. To justify our method theoretically, we show how the solution of the regularized optimal transport can be seen from the variational inference perspective thus motivating its use for co-clustering. The algorithm derived for the proposed method and its kernelized version based on the notion of Gromov-Wasserstein distance are fast, accurate and can determine automatically the number of both row and column clusters. These features are vividly demonstrated through extensive experimental evaluations.