Convex Non-negative Matrix Factorization Through Quantum Annealing
Paper and Code
Mar 28, 2022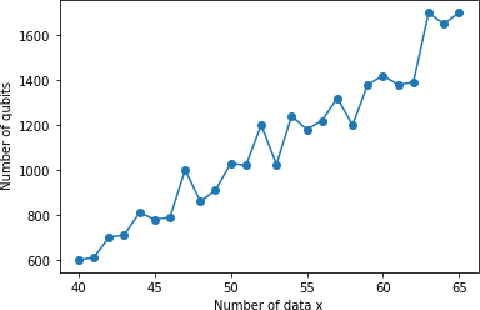

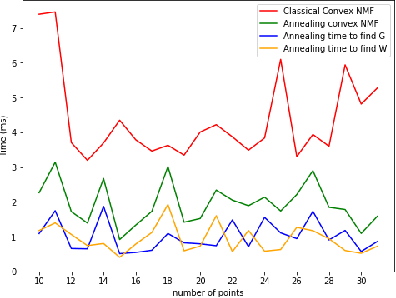
In this paper we provide the quantum version of the Convex Non-negative Matrix Factorization algorithm (Convex-NMF) by using the D-wave quantum annealer. More precisely, we use D-wave 2000Q to find the low rank approximation of a fixed real-valued matrix X by the product of two non-negative matrices factors W and G such that the Frobenius norm of the difference X-XWG is minimized. In order to solve this optimization problem we proceed in two steps. In the first step we transform the global real optimization problem depending on W,G into two quadratic unconstrained binary optimization problems (QUBO) depending on W and G respectively. In the second step we use an alternative strategy between the two QUBO problems corresponding to W and G to find the global solution. The running of these two QUBO problems on D-wave 2000Q need to use an embedding to the chimera graph of D-wave 2000Q, this embedding is limited by the number of qubits of D-wave 2000Q. We perform a study on the maximum number of real data to be used by our approach on D-wave 2000Q. The proposed study is based on the number of qubits used to represent each real variable. We also tested our approach on D-Wave 2000Q with several randomly generated data sets to prove that our approach is faster than the classical approach and also to prove that it gets the best results.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge