IM: An R-Package for Computation of Image Moments and Moment Invariants

Moment invariants are well-established and effective shape descriptors for image classification. In this report, we introduce a package for R-language, named IM, that implements the calculation of moments for images and allows the reconstruction of images from moments within an object-oriented framework. Several types of moments may be computed using the IM library, including discrete and continuous Chebyshev, Gegenbauer, Legendre, Krawtchouk, dual Hahn, generalized pseudo-Zernike, Fourier-Mellin, and radial harmonic Fourier moments. In addition, custom bivariate types of moments can be calculated using combinations of two different types of polynomials. A method of polar transformation of pixel coordinates is used to provide an approximate invariance to rotation for moments that are orthogonal over a rectangle. The different types of polynomials used to calculate moments are discussed in this report, as well as comparisons of reconstruction and running time. Examples of image classification using image moments are provided.

Generative modeling of the enteric nervous system employing point pattern analysis and graph construction

We describe a generative network model of the architecture of the enteric nervous system (ENS) in the colon employing data from images of human and mouse tissue samples obtained through confocal microscopy. Our models combine spatial point pattern analysis with graph generation to characterize the spatial and topological properties of the ganglia (clusters of neurons and glial cells), the inter-ganglionic connections, and the neuronal organization within the ganglia. We employ a hybrid hardcore-Strauss process for spatial patterns and a planar random graph generation for constructing the spatially embedded network. We show that our generative model may be helpful in both basic and translational studies, and it is sufficiently expressive to model the ENS architecture of individuals who vary in age and health status. Increased understanding of the ENS connectome will enable the use of neuromodulation strategies in treatment and clarify anatomic diagnostic criteria for people with bowel motility disorders.

A novel statistical methodology for quantifying the spatial arrangements of axons in peripheral nerves

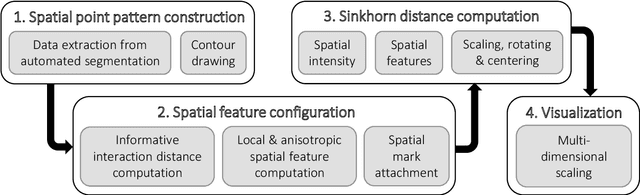
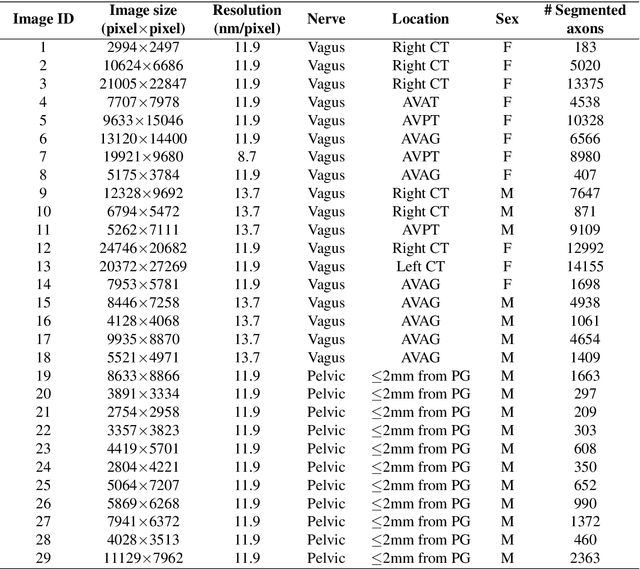
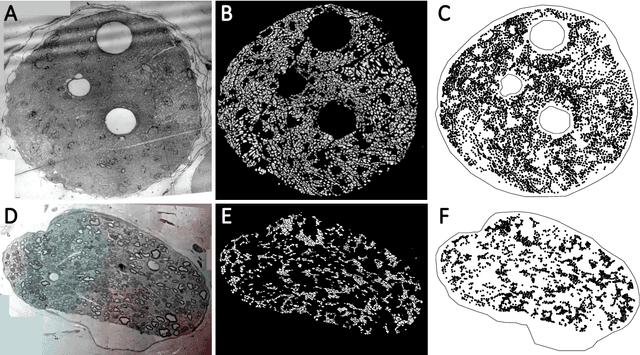
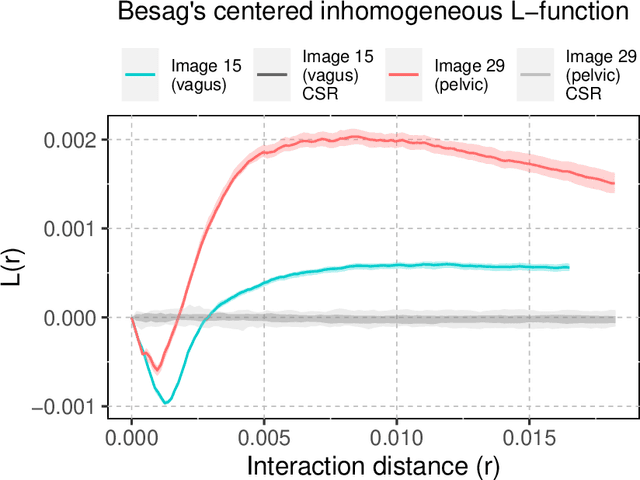
A thorough understanding of the neuroanatomy of peripheral nerves is required for a better insight into their function and the development of neuromodulation tools and strategies. In biophysical modeling, it is commonly assumed that the complex spatial arrangement of myelinated and unmyelinated axons in peripheral nerves is random, however, in reality the axonal organization is inhomogeneous and anisotropic. Present quantitative neuroanatomy methods analyze peripheral nerves in terms of the number of axons and the morphometric characteristics of the axons, such as area and diameter. In this study, we employed spatial statistics and point process models to describe the spatial arrangement of axons and Sinkhorn distances to compute the similarities between these arrangements (in terms of first- and second-order statistics) in various vagus and pelvic nerve cross-sections. We utilized high-resolution TEM images that have been segmented using a custom-built high-throughput deep learning system based on a highly modified U-Net architecture. Our findings show a novel and innovative approach to quantifying similarities between spatial point patterns using metrics derived from the solution to the optimal transport problem. We also present a generalizable pipeline for quantitative analysis of peripheral nerve architecture. Our data demonstrate differences between male- and female-originating samples and similarities between the pelvic and abdominal vagus nerves.

Bayesian Nonparametrics for Non-exhaustive Learning

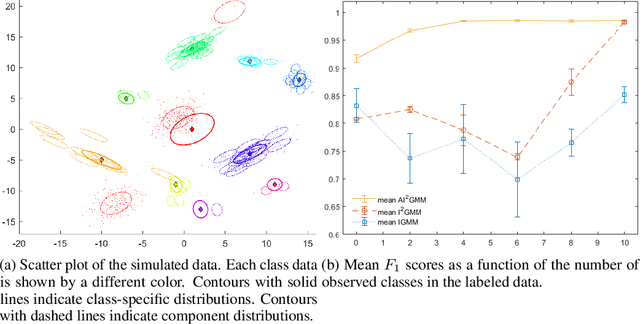
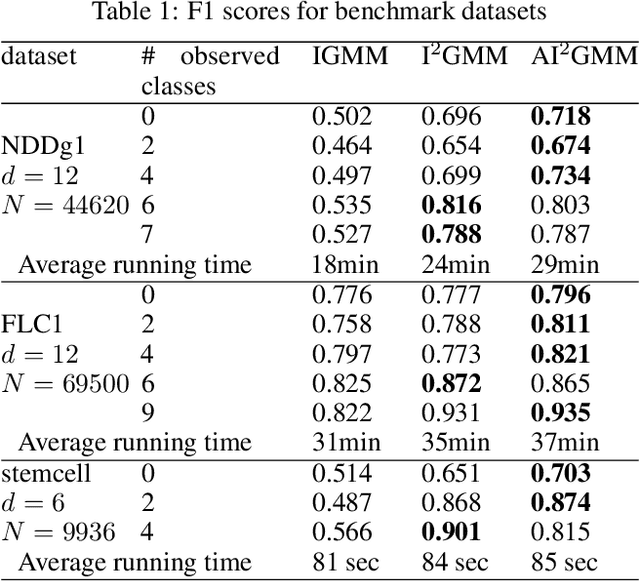
Non-exhaustive learning (NEL) is an emerging machine-learning paradigm designed to confront the challenge of non-stationary environments characterized by anon-exhaustive training sets lacking full information about the available classes.Unlike traditional supervised learning that relies on fixed models, NEL utilizes self-adjusting machine learning to better accommodate the non-stationary nature of the real-world problem, which is at the root of many recently discovered limitations of deep learning. Some of these hurdles led to a surge of interest in several research areas relevant to NEL such as open set classification or zero-shot learning. The presented study which has been motivated by two important applications proposes a NEL algorithm built on a highly flexible, doubly non-parametric Bayesian Gaussian mixture model that can grow arbitrarily large in terms of the number of classes and their components. We report several experiments that demonstrate the promising performance of the introduced model for NEL.

Scalable methods for nonnegative matrix factorizations of near-separable tall-and-skinny matrices

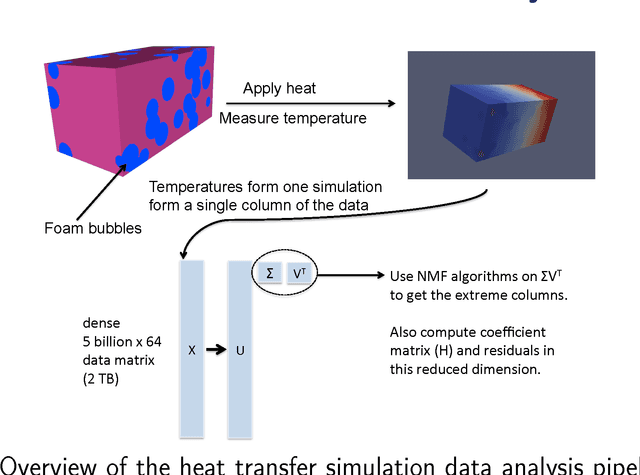
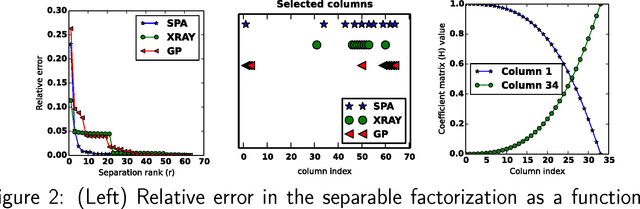
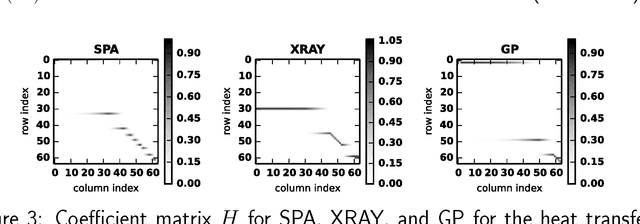
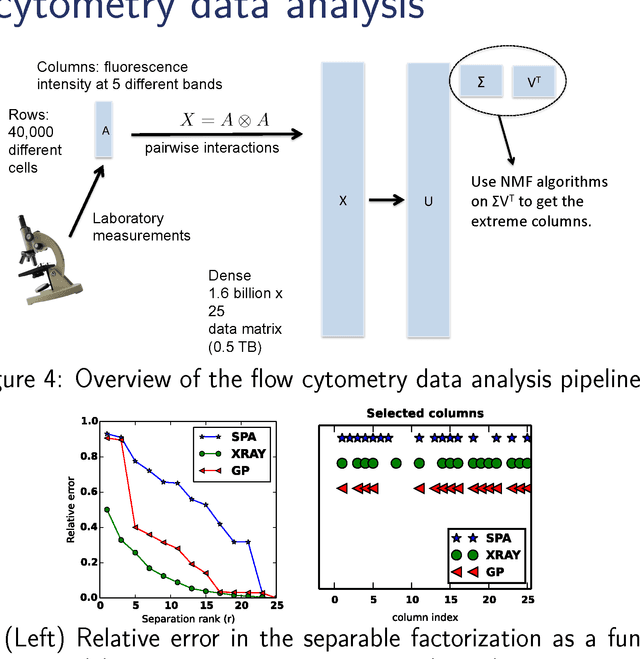
Numerous algorithms are used for nonnegative matrix factorization under the assumption that the matrix is nearly separable. In this paper, we show how to make these algorithms efficient for data matrices that have many more rows than columns, so-called "tall-and-skinny matrices". One key component to these improved methods is an orthogonal matrix transformation that preserves the separability of the NMF problem. Our final methods need a single pass over the data matrix and are suitable for streaming, multi-core, and MapReduce architectures. We demonstrate the efficacy of these algorithms on terabyte-sized synthetic matrices and real-world matrices from scientific computing and bioinformatics.

Bayesian Nonexhaustive Learning for Online Discovery and Modeling of Emerging Classes

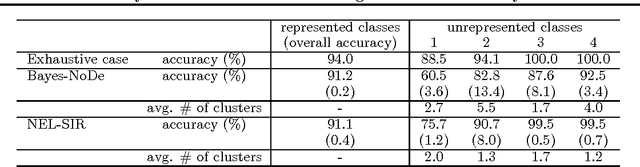
We present a framework for online inference in the presence of a nonexhaustively defined set of classes that incorporates supervised classification with class discovery and modeling. A Dirichlet process prior (DPP) model defined over class distributions ensures that both known and unknown class distributions originate according to a common base distribution. In an attempt to automatically discover potentially interesting class formations, the prior model is coupled with a suitably chosen data model, and sequential Monte Carlo sampling is used to perform online inference. Our research is driven by a biodetection application, where a new class of pathogen may suddenly appear, and the rapid increase in the number of samples originating from this class indicates the onset of an outbreak.