IM: An R-Package for Computation of Image Moments and Moment Invariants

Moment invariants are well-established and effective shape descriptors for image classification. In this report, we introduce a package for R-language, named IM, that implements the calculation of moments for images and allows the reconstruction of images from moments within an object-oriented framework. Several types of moments may be computed using the IM library, including discrete and continuous Chebyshev, Gegenbauer, Legendre, Krawtchouk, dual Hahn, generalized pseudo-Zernike, Fourier-Mellin, and radial harmonic Fourier moments. In addition, custom bivariate types of moments can be calculated using combinations of two different types of polynomials. A method of polar transformation of pixel coordinates is used to provide an approximate invariance to rotation for moments that are orthogonal over a rectangle. The different types of polynomials used to calculate moments are discussed in this report, as well as comparisons of reconstruction and running time. Examples of image classification using image moments are provided.

A novel statistical methodology for quantifying the spatial arrangements of axons in peripheral nerves

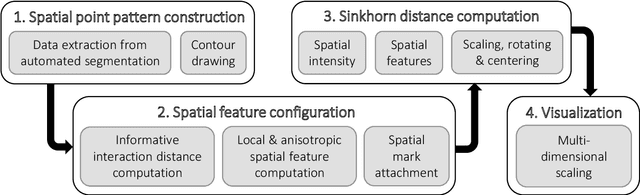
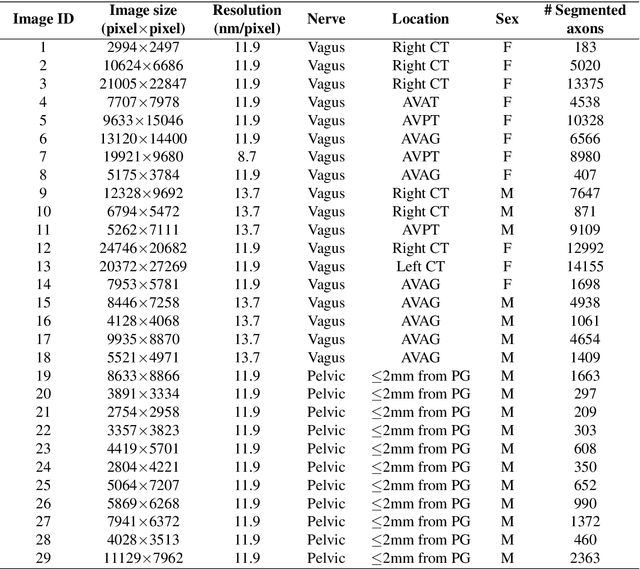
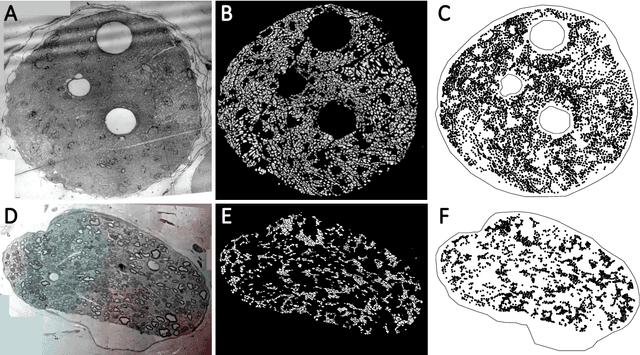
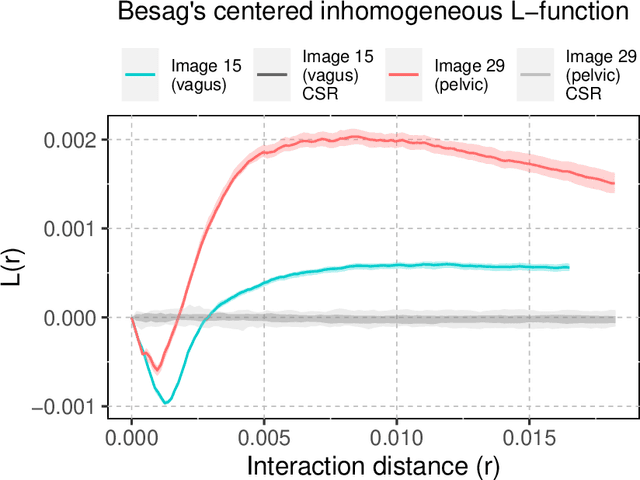
A thorough understanding of the neuroanatomy of peripheral nerves is required for a better insight into their function and the development of neuromodulation tools and strategies. In biophysical modeling, it is commonly assumed that the complex spatial arrangement of myelinated and unmyelinated axons in peripheral nerves is random, however, in reality the axonal organization is inhomogeneous and anisotropic. Present quantitative neuroanatomy methods analyze peripheral nerves in terms of the number of axons and the morphometric characteristics of the axons, such as area and diameter. In this study, we employed spatial statistics and point process models to describe the spatial arrangement of axons and Sinkhorn distances to compute the similarities between these arrangements (in terms of first- and second-order statistics) in various vagus and pelvic nerve cross-sections. We utilized high-resolution TEM images that have been segmented using a custom-built high-throughput deep learning system based on a highly modified U-Net architecture. Our findings show a novel and innovative approach to quantifying similarities between spatial point patterns using metrics derived from the solution to the optimal transport problem. We also present a generalizable pipeline for quantitative analysis of peripheral nerve architecture. Our data demonstrate differences between male- and female-originating samples and similarities between the pelvic and abdominal vagus nerves.