DONUT-hole: DONUT Sparsification by Harnessing Knowledge and Optimizing Learning Efficiency

This paper introduces DONUT-hole, a sparse OCR-free visual document understanding (VDU) model that addresses the limitations of its predecessor model, dubbed DONUT. The DONUT model, leveraging a transformer architecture, overcoming the challenges of separate optical character recognition (OCR) and visual semantic understanding (VSU) components. However, its deployment in production environments and edge devices is hindered by high memory and computational demands, particularly in large-scale request services. To overcome these challenges, we propose an optimization strategy based on knowledge distillation and model pruning. Our paradigm to produce DONUT-hole, reduces the model denisty by 54\% while preserving performance. We also achieve a global representational similarity index between DONUT and DONUT-hole based on centered kernel alignment (CKA) metric of 0.79. Moreover, we evaluate the effectiveness of DONUT-hole in the document image key information extraction (KIE) task, highlighting its potential for developing more efficient VDU systems for logistic companies.

Learn to Bind and Grow Neural Structures

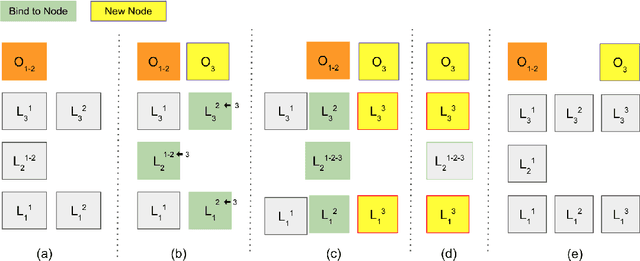
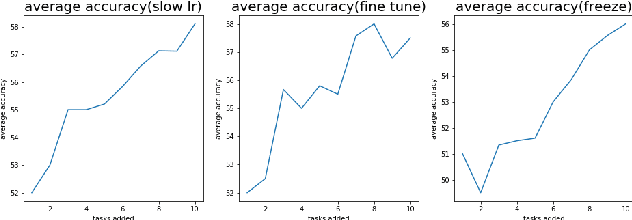
Task-incremental learning involves the challenging problem of learning new tasks continually, without forgetting past knowledge. Many approaches address the problem by expanding the structure of a shared neural network as tasks arrive, but struggle to grow optimally, without losing past knowledge. We present a new framework, Learn to Bind and Grow, which learns a neural architecture for a new task incrementally, either by binding with layers of a similar task or by expanding layers which are more likely to conflict between tasks. Central to our approach is a novel, interpretable, parameterization of the shared, multi-task architecture space, which then enables computing globally optimal architectures using Bayesian optimization. Experiments on continual learning benchmarks show that our framework performs comparably with earlier expansion based approaches and is able to flexibly compute multiple optimal solutions with performance-size trade-offs.

Parsimonious Computing: A Minority Training Regime for Effective Prediction in Large Microarray Expression Data Sets

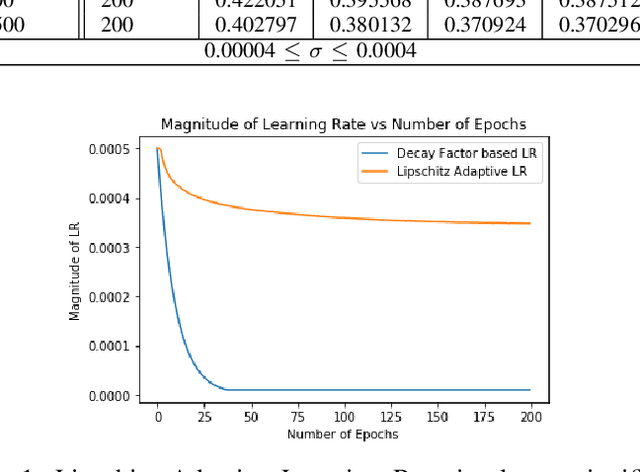
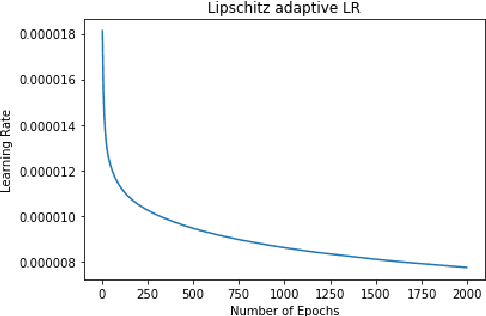
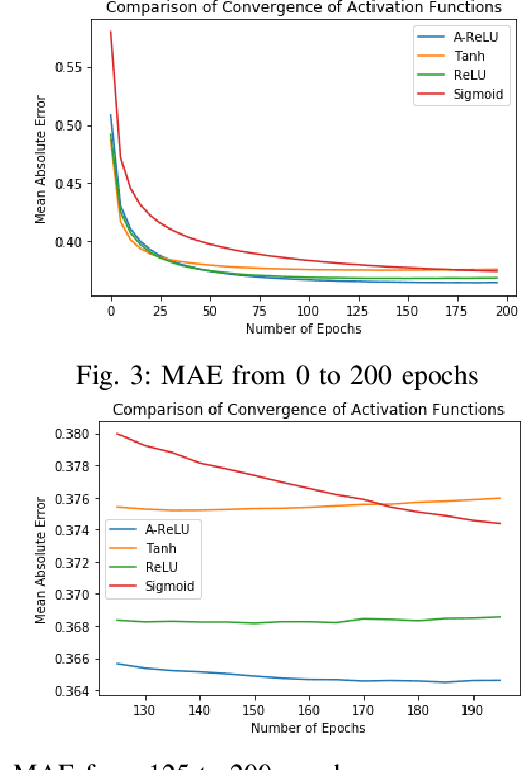
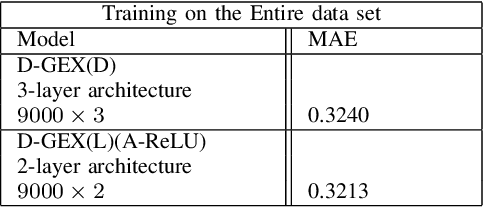
Rigorous mathematical investigation of learning rates used in back-propagation in shallow neural networks has become a necessity. This is because experimental evidence needs to be endorsed by a theoretical background. Such theory may be helpful in reducing the volume of experimental effort to accomplish desired results. We leveraged the functional property of Mean Square Error, which is Lipschitz continuous to compute learning rate in shallow neural networks. We claim that our approach reduces tuning efforts, especially when a significant corpus of data has to be handled. We achieve remarkable improvement in saving computational cost while surpassing prediction accuracy reported in literature. The learning rate, proposed here, is the inverse of the Lipschitz constant. The work results in a novel method for carrying out gene expression inference on large microarray data sets with a shallow architecture constrained by limited computing resources. A combination of random sub-sampling of the dataset, an adaptive Lipschitz constant inspired learning rate and a new activation function, A-ReLU helped accomplish the results reported in the paper.