Set-Structured Latent Representations

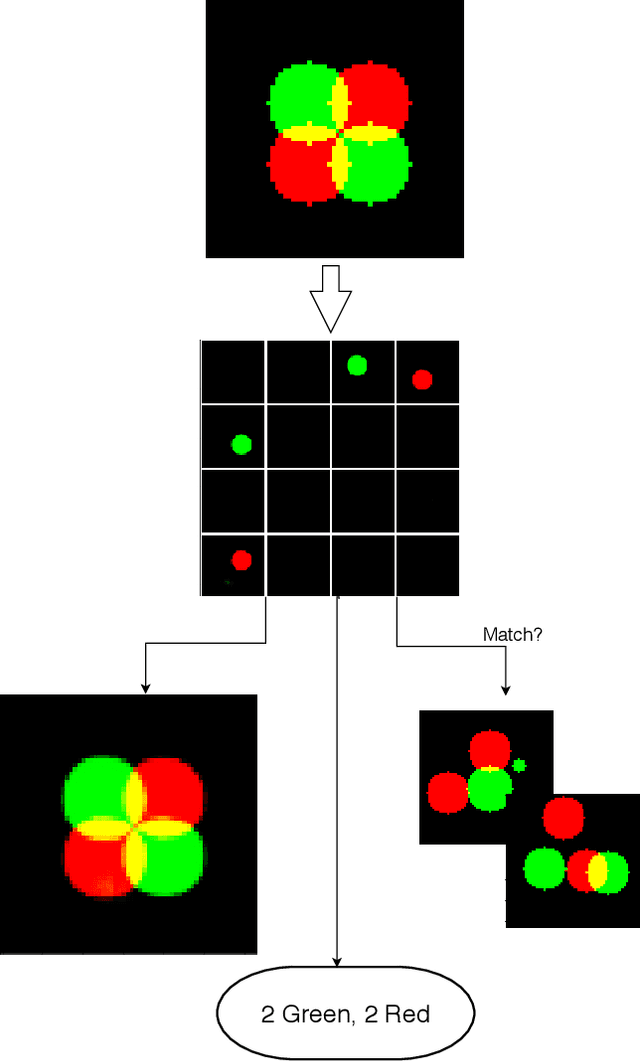
Unstructured data often has latent component structure, such as the objects in an image of a scene. In these situations, the relevant latent structure is an unordered collection or \emph{set}. However, learning such representations directly from data is difficult due to the discrete and unordered structure. Here, we develop a framework for differentiable learning of set-structured latent representations. We show how to use this framework to naturally decompose data such as images into sets of interpretable and meaningful components and demonstrate how existing techniques cannot properly disentangle relevant structure. We also show how to extend our methodology to downstream tasks such as set matching, which uses set-specific operations. Our code is available at https://github.com/CUVL/SSLR.

Outcome Correlation in Graph Neural Network Regression

Graph neural networks aggregate features in vertex neighborhoods to learn vector representations of all vertices, using supervision from some labeled vertices during training. The predictor is then a function of the vector representation, and predictions are made independently on unlabeled nodes. This widely-adopted approach implicitly assumes that vertex labels are independent after conditioning on their neighborhoods. We show that this strong assumption is far from true on many real-world graph datasets and severely limits predictive power on a number of regression tasks. Given that traditional graph-based semi-supervised learning methods operate in the opposite manner by explicitly modeling the correlation in predicted outcomes, this limitation may not be all that surprising. Here, we address this issue with a simple and interpretable framework that can improve any graph neural network architecture by modeling correlation structure in regression outcome residuals. Specifically, we model the joint distribution of outcome residuals on vertices with a parameterized multivariate Gaussian, where the parameters are estimated by maximizing the marginal likelihood of the observed labels. Our model achieves substantially boosts the performance of graph neural networks, and the learned parameters can also be interpreted as the strength of correlation among connected vertices. To allow us to scale to large networks, we design linear time algorithms for low-variance, unbiased model parameter estimates based on stochastic trace estimation. We also provide a simplified version of our method that makes stronger assumptions on correlation structure but is extremely easy to implement and provides great practical performance in several cases.