Stochastic Primal Dual Coordinate Method with Non-Uniform Sampling Based on Optimality Violations

We study primal-dual type stochastic optimization algorithms with non-uniform sampling. Our main theoretical contribution in this paper is to present a convergence analysis of Stochastic Primal Dual Coordinate (SPDC) Method with arbitrary sampling. Based on this theoretical framework, we propose Optimality Violation-based Sampling SPDC (ovsSPDC), a non-uniform sampling method based on Optimality Violation. We also propose two efficient heuristic variants of ovsSPDC called ovsSDPC+ and ovsSDPC++. Through intensive numerical experiments, we demonstrate that the proposed method and its variants are faster than other state-of-the-art primal-dual type stochastic optimization methods.

Efficiently Bounding Optimal Solutions after Small Data Modification in Large-Scale Empirical Risk Minimization

We study large-scale classification problems in changing environments where a small part of the dataset is modified, and the effect of the data modification must be quickly incorporated into the classifier. When the entire dataset is large, even if the amount of the data modification is fairly small, the computational cost of re-training the classifier would be prohibitively large. In this paper, we propose a novel method for efficiently incorporating such a data modification effect into the classifier without actually re-training it. The proposed method provides bounds on the unknown optimal classifier with the cost only proportional to the size of the data modification. We demonstrate through numerical experiments that the proposed method provides sufficiently tight bounds with negligible computational costs, especially when a small part of the dataset is modified in a large-scale classification problem.

Simultaneous Safe Screening of Features and Samples in Doubly Sparse Modeling

The problem of learning a sparse model is conceptually interpreted as the process of identifying active features/samples and then optimizing the model over them. Recently introduced safe screening allows us to identify a part of non-active features/samples. So far, safe screening has been individually studied either for feature screening or for sample screening. In this paper, we introduce a new approach for safely screening features and samples simultaneously by alternatively iterating feature and sample screening steps. A significant advantage of considering them simultaneously rather than individually is that they have a synergy effect in the sense that the results of the previous safe feature screening can be exploited for improving the next safe sample screening performances, and vice-versa. We first theoretically investigate the synergy effect, and then illustrate the practical advantage through intensive numerical experiments for problems with large numbers of features and samples.

Regularization Path of Cross-Validation Error Lower Bounds

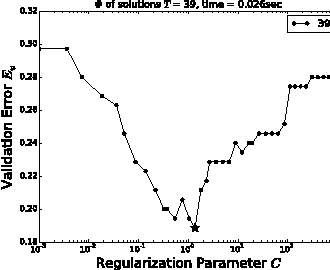
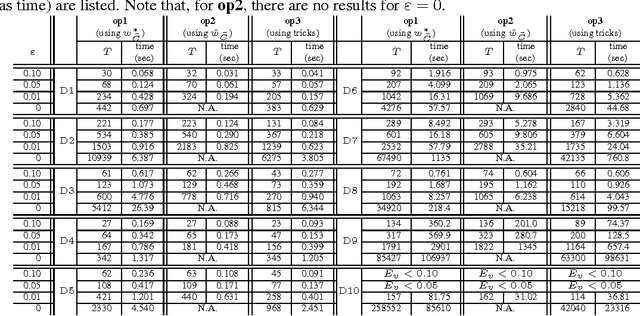
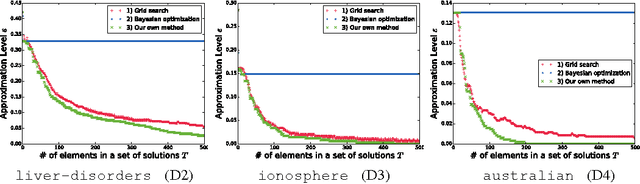
Careful tuning of a regularization parameter is indispensable in many machine learning tasks because it has a significant impact on generalization performances. Nevertheless, current practice of regularization parameter tuning is more of an art than a science, e.g., it is hard to tell how many grid-points would be needed in cross-validation (CV) for obtaining a solution with sufficiently small CV error. In this paper we propose a novel framework for computing a lower bound of the CV errors as a function of the regularization parameter, which we call regularization path of CV error lower bounds. The proposed framework can be used for providing a theoretical approximation guarantee on a set of solutions in the sense that how far the CV error of the current best solution could be away from best possible CV error in the entire range of the regularization parameters. We demonstrate through numerical experiments that a theoretically guaranteed a choice of regularization parameter in the above sense is possible with reasonable computational costs.