Regularization Path of Cross-Validation Error Lower Bounds
Paper and Code
Jun 22, 2015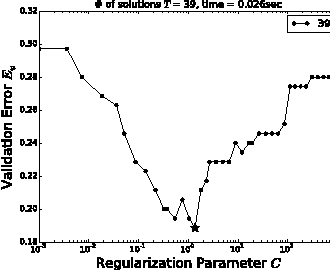
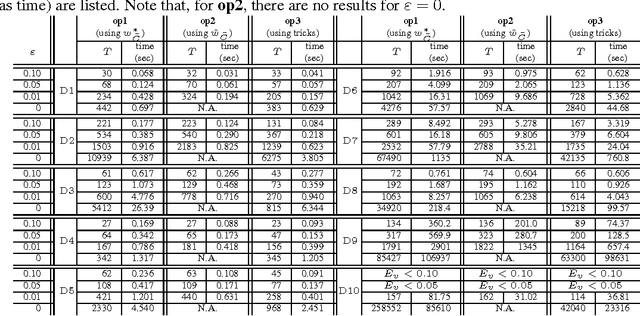
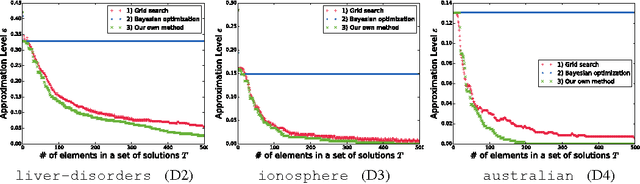

Careful tuning of a regularization parameter is indispensable in many machine learning tasks because it has a significant impact on generalization performances. Nevertheless, current practice of regularization parameter tuning is more of an art than a science, e.g., it is hard to tell how many grid-points would be needed in cross-validation (CV) for obtaining a solution with sufficiently small CV error. In this paper we propose a novel framework for computing a lower bound of the CV errors as a function of the regularization parameter, which we call regularization path of CV error lower bounds. The proposed framework can be used for providing a theoretical approximation guarantee on a set of solutions in the sense that how far the CV error of the current best solution could be away from best possible CV error in the entire range of the regularization parameters. We demonstrate through numerical experiments that a theoretically guaranteed a choice of regularization parameter in the above sense is possible with reasonable computational costs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge