Distributed Assignment with Limited Communication for Multi-Robot Multi-Target Tracking

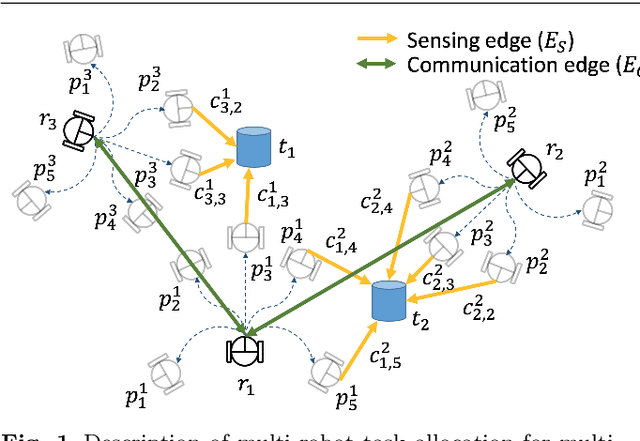
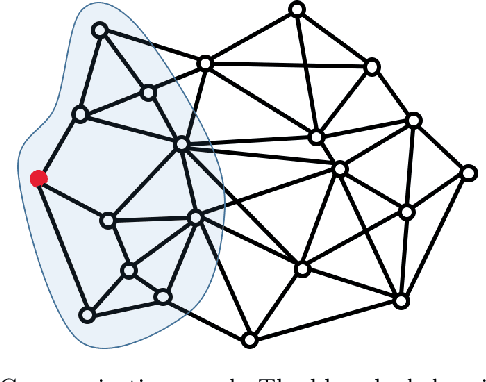
We study the problem of tracking multiple moving targets using a team of mobile robots. Each robot has a set of motion primitives to choose from in order to collectively maximize the number of targets tracked or the total quality of tracking. Our focus is on scenarios where communication is limited and the robots have limited time to share information with their neighbors. As a result, we seek distributed algorithms that can find solutions in bounded amount of time. We present two algorithms: (1) a greedy algorithm that is guaranteed finds a $2$-approximation to the optimal (centralized) solution albeit requiring $|R|$ communication rounds in the worst-case, where $|R|$ denotes the number of robots; and (2) a local algorithm that finds a $\mathcal{O}\left((1+\epsilon)(1+1/h)\right)$-approximation algorithm in $\mathcal{O}(h\log 1/\epsilon)$ communication rounds. Here, $h$ and $\epsilon$ are parameters that allow the user to trade-off the solution quality with communication time. In addition to theoretical results, we present empirical evaluation including comparisons with centralized optimal solutions.

Distributed Simultaneous Action and Target Assignment for Multi-Robot Multi-Target Tracking

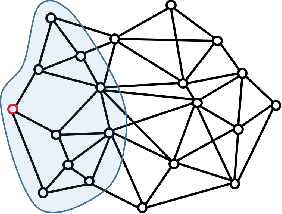
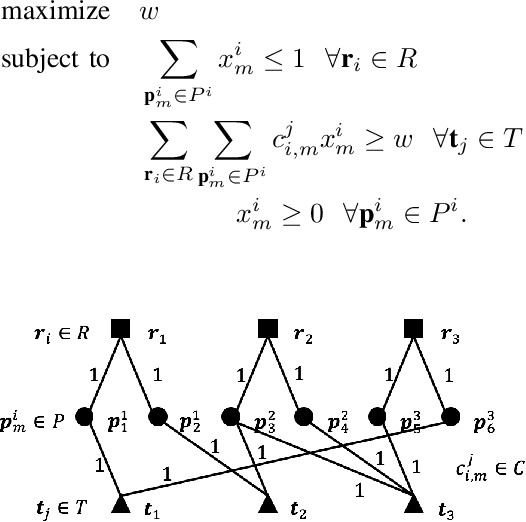
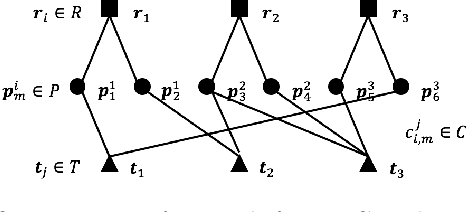
We study a multi-robot assignment problem for multi-target tracking. The proposed problem can be viewed as the mixed packing and covering problem. To deal with a limitation on both sensing and communication ranges, a distributed approach is taken into consideration. A local algorithm gives theoretical bounds on both the running time and approximation ratio to an optimal solution. We employ a local algorithm of max-min linear programs to solve the proposed task. Simulation result shows that a local algorithm is an effective solution to the multi-robot task allocation.

Algorithms for Routing of Unmanned Aerial Vehicles with Mobile Recharging Stations

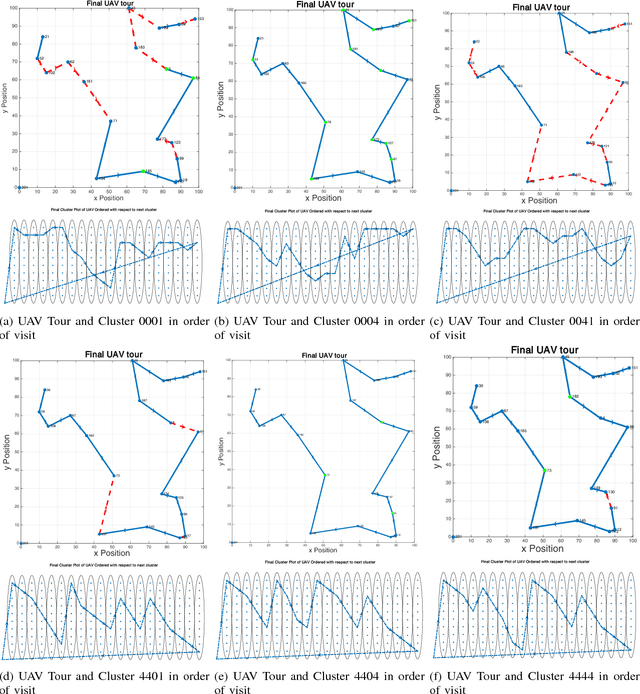
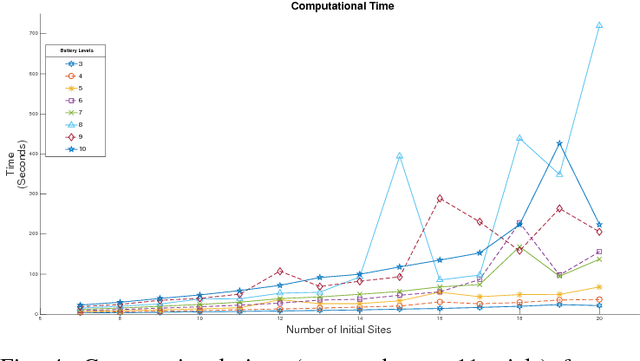
We study the problem of planning a tour for an energy-limited Unmanned Aerial Vehicle (UAV) to visit a set of sites in the least amount of time. We envision scenarios where the UAV can be recharged along the way either by landing on stationary recharging stations or on Unmanned Ground Vehicles (UGVs) acting as mobile recharging stations. This leads to a new variant of the Traveling Salesperson Problem (TSP) with mobile recharging stations. We present an algorithm that finds not only the order in which to visit the sites but also when and where to land on the charging stations to recharge. Our algorithm plans tours for the UGVs as well as determines best locations to place stationary charging stations. While the problems we study are NP-Hard, we present a practical solution using Generalized TSP that finds the optimal solution. If the UGVs are slower, the algorithm also finds the minimum number of UGVs required to support the UAV mission such that the UAV is not required to wait for the UGV. Our simulation results show that the running time is acceptable for reasonably sized instances in practice.

Algorithms for Visibility-Based Monitoring with Robot Teams

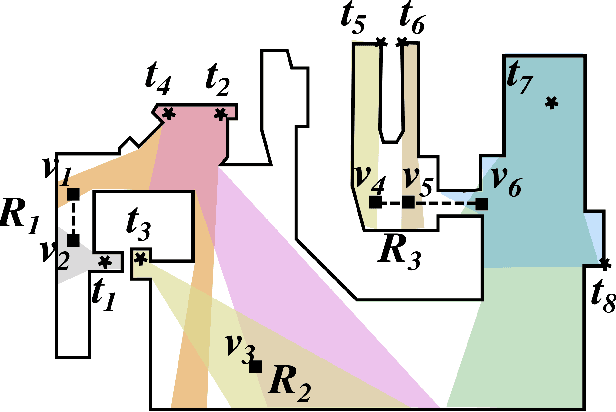
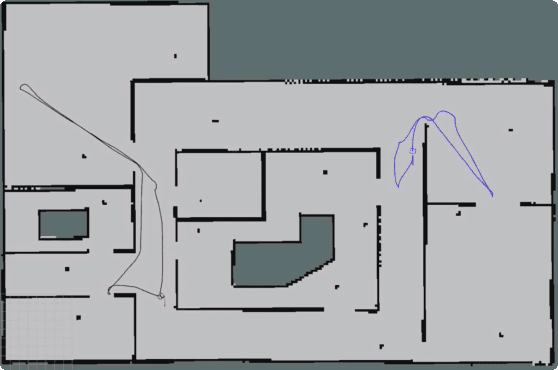
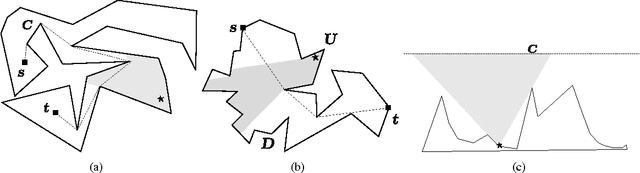
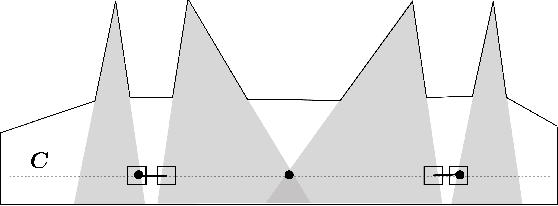
We study the problem of planning paths for a team of robots for visually monitoring an environment. Our work is motivated by surveillance and persistent monitoring applications. We are given a set of target points in a polygonal environment that must be monitored using robots with cameras. The goal is to compute paths for all robots such that every target is visible from at least one path. In its general form, this problem is NP-hard as it generalizes the Art Gallery Problem and the Watchman Route Problem. We study two versions: (i) a geometric version in \emph{street polygons} for which we give a polynomial time $4$--approximation algorithm; and (ii) a general version for which we present a practical solution that finds the optimal solution in possibly exponential time. In addition to theoretical proofs, we also present results from simulation studies.