Algorithms for Visibility-Based Monitoring with Robot Teams
Paper and Code
Dec 10, 2016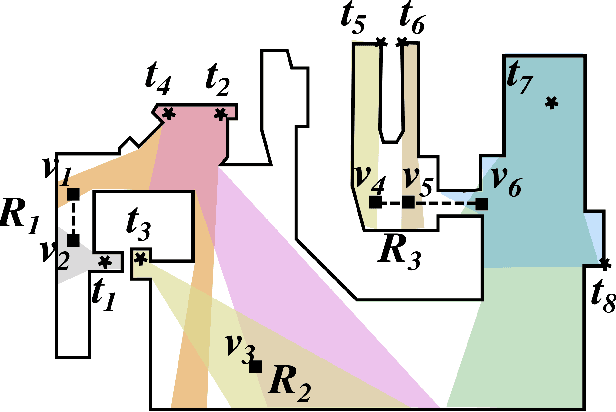
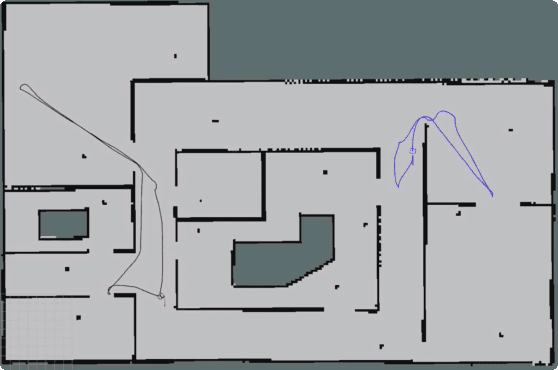
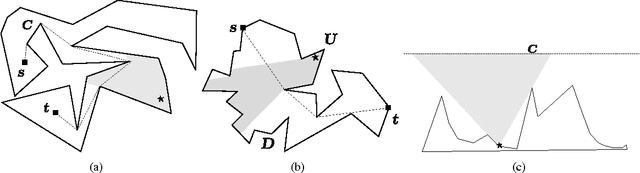
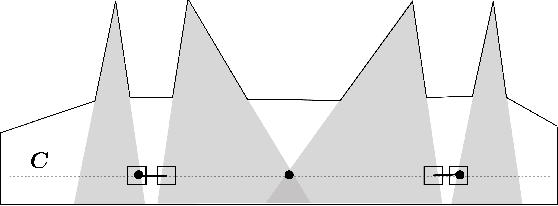
We study the problem of planning paths for a team of robots for visually monitoring an environment. Our work is motivated by surveillance and persistent monitoring applications. We are given a set of target points in a polygonal environment that must be monitored using robots with cameras. The goal is to compute paths for all robots such that every target is visible from at least one path. In its general form, this problem is NP-hard as it generalizes the Art Gallery Problem and the Watchman Route Problem. We study two versions: (i) a geometric version in \emph{street polygons} for which we give a polynomial time $4$--approximation algorithm; and (ii) a general version for which we present a practical solution that finds the optimal solution in possibly exponential time. In addition to theoretical proofs, we also present results from simulation studies.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge