Arvind Thiagarajan
Challenges and approaches to privacy preserving post-click conversion prediction
Jan 29, 2022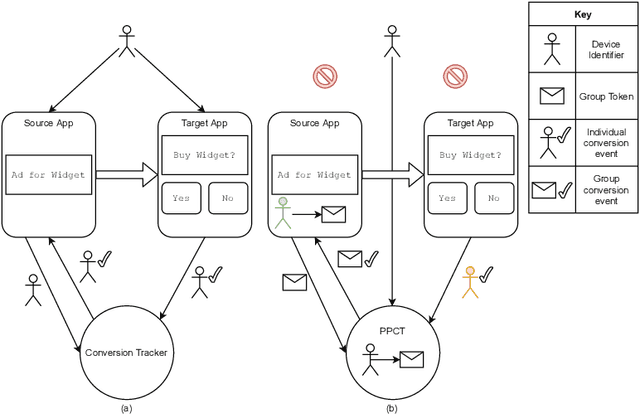
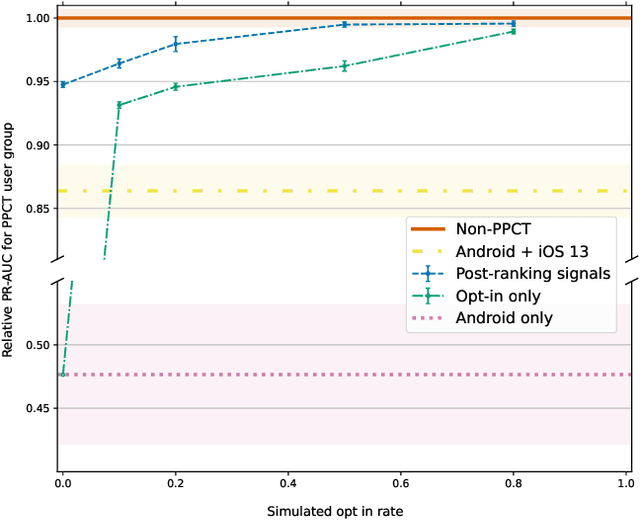
Abstract:Online advertising has typically been more personalized than offline advertising, through the use of machine learning models and real-time auctions for ad targeting. One specific task, predicting the likelihood of conversion (i.e.\ the probability a user will purchase the advertised product), is crucial to the advertising ecosystem for both targeting and pricing ads. Currently, these models are often trained by observing individual user behavior, but, increasingly, regulatory and technical constraints are requiring privacy-preserving approaches. For example, major platforms are moving to restrict tracking individual user events across multiple applications, and governments around the world have shown steadily more interest in regulating the use of personal data. Instead of receiving data about individual user behavior, advertisers may receive privacy-preserving feedback, such as the number of installs of an advertised app that resulted from a group of users. In this paper we outline the recent privacy-related changes in the online advertising ecosystem from a machine learning perspective. We provide an overview of the challenges and constraints when learning conversion models in this setting. We introduce a novel approach for training these models that makes use of post-ranking signals. We show using offline experiments on real world data that it outperforms a model relying on opt-in data alone, and significantly reduces model degradation when no individual labels are available. Finally, we discuss future directions for research in this evolving area.
Using Weighted P-Values in Fisher's Method
Jun 17, 2020Abstract:Fisher's method prescribes a way to combine p-values from multiple experiments into a single p-value. However, the original method can only determine a combined p-value analytically if all constituent p-values are weighted equally. Here we present, with proof, a method to combine p-values with arbitrary weights.
Improvements in Computation and Usage of Joint CDFs for the N-Dimensional Order Statistic
Jun 17, 2020Abstract:Order statistics provide an intuition for combining multiple lists of scores over a common index set. This intuition is particularly valuable when the lists to be combined cannot be directly compared in a sensible way. We describe here the advantages of a new method for using joint CDFs of such order statistics to combine score lists. We also present, with proof, a new algorithm for computing such joint CDF values, with runtime linear in the size of the combined list.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge