Loop-Diffusion: an equivariant diffusion model for designing and scoring protein loops

Predicting protein functional characteristics from structure remains a central problem in protein science, with broad implications from understanding the mechanisms of disease to designing novel therapeutics. Unfortunately, current machine learning methods are limited by scarce and biased experimental data, and physics-based methods are either too slow to be useful, or too simplified to be accurate. In this work, we present Loop-Diffusion, an energy based diffusion model which leverages a dataset of general protein loops from the entire protein universe to learn an energy function that generalizes to functional prediction tasks. We evaluate Loop-Diffusion's performance on scoring TCR-pMHC interfaces and demonstrate state-of-the-art results in recognizing binding-enhancing mutations.

HERMES: Holographic Equivariant neuRal network model for Mutational Effect and Stability prediction

Predicting the stability and fitness effects of amino acid mutations in proteins is a cornerstone of biological discovery and engineering. Various experimental techniques have been developed to measure mutational effects, providing us with extensive datasets across a diverse range of proteins. By training on these data, traditional computational modeling and more recent machine learning approaches have advanced significantly in predicting mutational effects. Here, we introduce HERMES, a 3D rotationally equivariant structure-based neural network model for mutational effect and stability prediction. Pre-trained to predict amino acid propensity from its surrounding 3D structure, HERMES can be fine-tuned for mutational effects using our open-source code. We present a suite of HERMES models, pre-trained with different strategies, and fine-tuned to predict the stability effect of mutations. Benchmarking against other models shows that HERMES often outperforms or matches their performance in predicting mutational effect on stability, binding, and fitness. HERMES offers versatile tools for evaluating mutational effects and can be fine-tuned for specific predictive objectives.

H-Packer: Holographic Rotationally Equivariant Convolutional Neural Network for Protein Side-Chain Packing

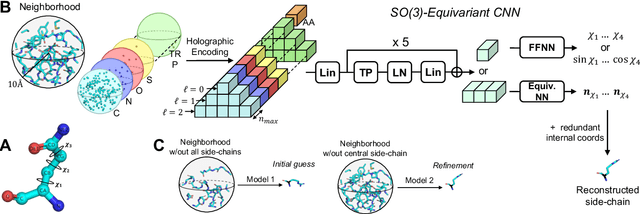
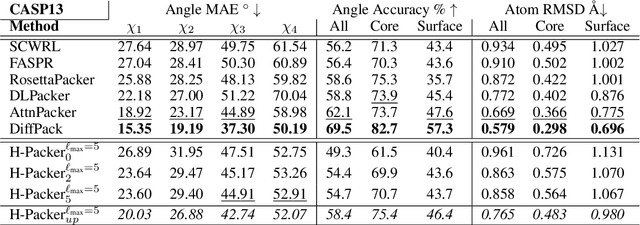
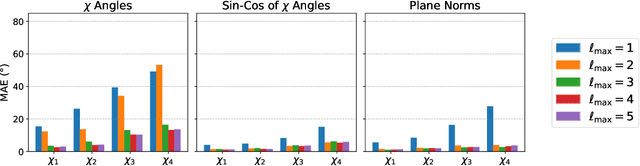
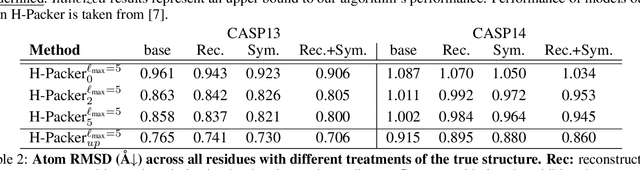
Accurately modeling protein 3D structure is essential for the design of functional proteins. An important sub-task of structure modeling is protein side-chain packing: predicting the conformation of side-chains (rotamers) given the protein's backbone structure and amino-acid sequence. Conventional approaches for this task rely on expensive sampling procedures over hand-crafted energy functions and rotamer libraries. Recently, several deep learning methods have been developed to tackle the problem in a data-driven way, albeit with vastly different formulations (from image-to-image translation to directly predicting atomic coordinates). Here, we frame the problem as a joint regression over the side-chains' true degrees of freedom: the dihedral $\chi$ angles. We carefully study possible objective functions for this task, while accounting for the underlying symmetries of the task. We propose Holographic Packer (H-Packer), a novel two-stage algorithm for side-chain packing built on top of two light-weight rotationally equivariant neural networks. We evaluate our method on CASP13 and CASP14 targets. H-Packer is computationally efficient and shows favorable performance against conventional physics-based algorithms and is competitive against alternative deep learning solutions.

Learning the shape of protein micro-environments with a holographic convolutional neural network

Proteins play a central role in biology from immune recognition to brain activity. While major advances in machine learning have improved our ability to predict protein structure from sequence, determining protein function from structure remains a major challenge. Here, we introduce Holographic Convolutional Neural Network (H-CNN) for proteins, which is a physically motivated machine learning approach to model amino acid preferences in protein structures. H-CNN reflects physical interactions in a protein structure and recapitulates the functional information stored in evolutionary data. H-CNN accurately predicts the impact of mutations on protein function, including stability and binding of protein complexes. Our interpretable computational model for protein structure-function maps could guide design of novel proteins with desired function.

Holographic-AE: an end-to-end SO-Equivariant Autoencoder in Fourier Space

Group-equivariant neural networks have emerged as a data-efficient approach to solve classification and regression tasks, while respecting the relevant symmetries of the data. However, little work has been done to extend this paradigm to the unsupervised and generative domains. Here, we present Holographic-(V)AE (H-(V)AE), a fully end-to-end SO(3)-equivariant (variational) autoencoder in Fourier space, suitable for unsupervised learning and generation of data distributed around a specified origin. H-(V)AE is trained to reconstruct the spherical Fourier encoding of data, learning in the process a latent space with a maximally informative invariant embedding alongside an equivariant frame describing the orientation of the data. We extensively test the performance of H-(V)AE on diverse datasets and show that its latent space efficiently encodes the categorical features of spherical images and structural features of protein atomic environments. Our work can further be seen as a case study for equivariant modeling of a data distribution by reconstructing its Fourier encoding.

MINIMALIST: Mutual INformatIon Maximization for Amortized Likelihood Inference from Sampled Trajectories

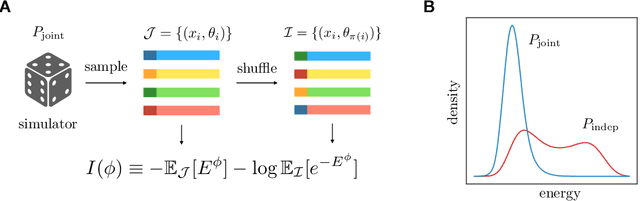
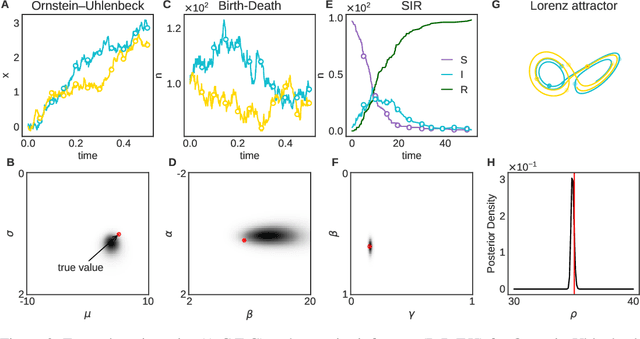
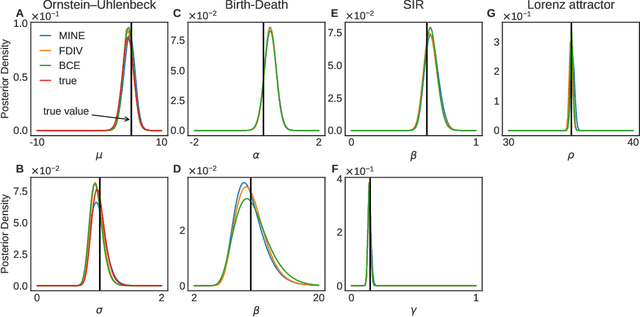
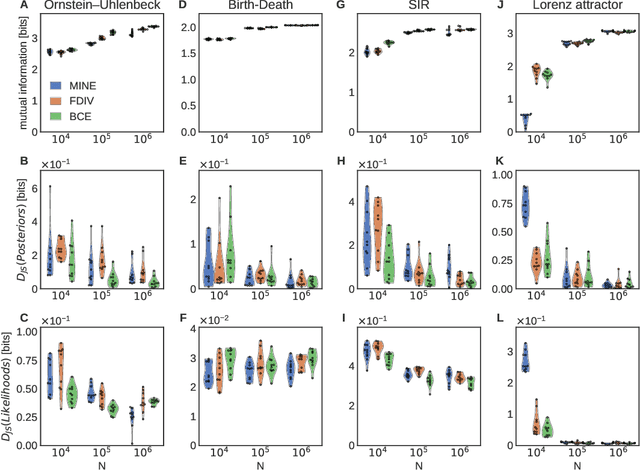
Simulation-based inference enables learning the parameters of a model even when its likelihood cannot be computed in practice. One class of methods uses data simulated with different parameters to infer an amortized estimator for the likelihood-to-evidence ratio, or equivalently the posterior function. We show that this approach can be formulated in terms of mutual information maximization between model parameters and simulated data. We use this equivalence to reinterpret existing approaches for amortized inference, and propose two new methods that rely on lower bounds of the mutual information. We apply our framework to the inference of parameters of stochastic processes and chaotic dynamical systems from sampled trajectories, using artificial neural networks for posterior prediction. Our approach provides a unified framework that leverages the power of mutual information estimators for inference.