MINIMALIST: Mutual INformatIon Maximization for Amortized Likelihood Inference from Sampled Trajectories

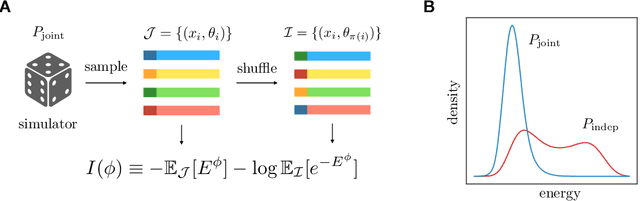
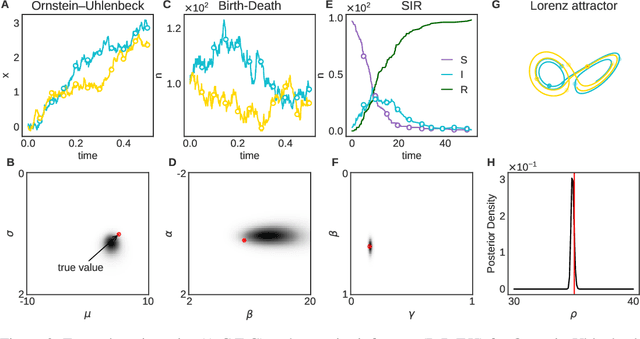
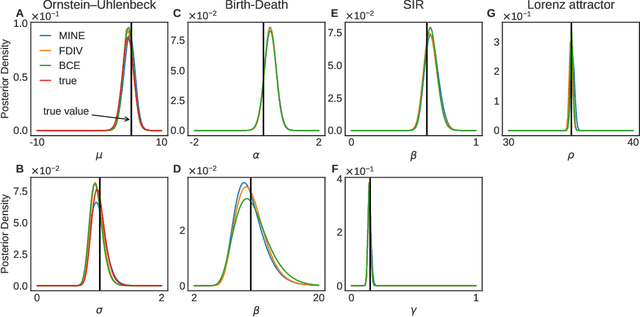
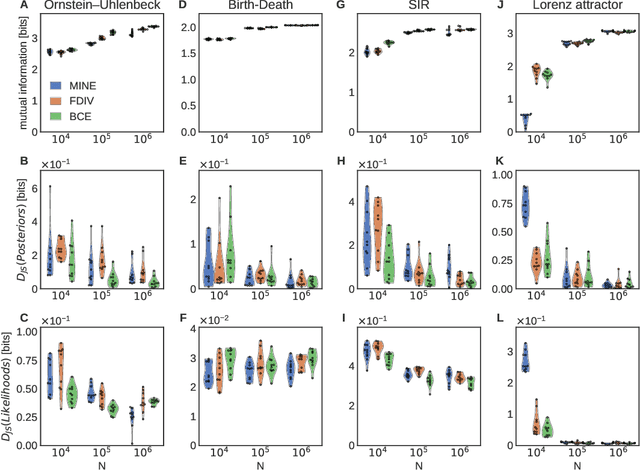
Simulation-based inference enables learning the parameters of a model even when its likelihood cannot be computed in practice. One class of methods uses data simulated with different parameters to infer an amortized estimator for the likelihood-to-evidence ratio, or equivalently the posterior function. We show that this approach can be formulated in terms of mutual information maximization between model parameters and simulated data. We use this equivalence to reinterpret existing approaches for amortized inference, and propose two new methods that rely on lower bounds of the mutual information. We apply our framework to the inference of parameters of stochastic processes and chaotic dynamical systems from sampled trajectories, using artificial neural networks for posterior prediction. Our approach provides a unified framework that leverages the power of mutual information estimators for inference.

Flocking and turning: a new model for self-organized collective motion

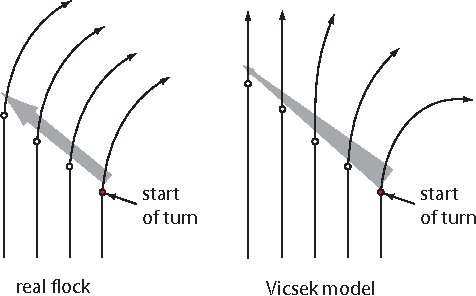
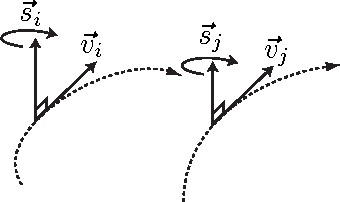
Birds in a flock move in a correlated way, resulting in large polarization of velocities. A good understanding of this collective behavior exists for linear motion of the flock. Yet observing actual birds, the center of mass of the group often turns giving rise to more complicated dynamics, still keeping strong polarization of the flock. Here we propose novel dynamical equations for the collective motion of polarized animal groups that account for correlated turning including solely social forces. We exploit rotational symmetries and conservation laws of the problem to formulate a theory in terms of generalized coordinates of motion for the velocity directions akin to a Hamiltonian formulation for rotations. We explicitly derive the correspondence between this formulation and the dynamics of the individual velocities, thus obtaining a new model of collective motion. In the appropriate overdamped limit we recover the well-known Vicsek model, which dissipates rotational information and does not allow for polarized turns. Although the new model has its most vivid success in describing turning groups, its dynamics is intrinsically different from previous ones in a wide dynamical regime, while reducing to the hydrodynamic description of Toner and Tu at very large length-scales. The derived framework is therefore general and it may describe the collective motion of any strongly polarized active matter system.