Towards a tracking algorithm based on the clustering of spatio-temporal clouds of points

The interest in 3D dynamical tracking is growing in fields such as robotics, biology and fluid dynamics. Recently, a major source of progress in 3D tracking has been the study of collective behaviour in biological systems, where the trajectories of individual animals moving within large and dense groups need to be reconstructed to understand the behavioural interaction rules. Experimental data in this field are generally noisy and at low spatial resolution, so that individuals appear as small featureless objects and trajectories must be retrieved by making use of epipolar information only. Moreover, optical occlusions often occur: in a multi-camera system one or more objects become indistinguishable in one view, potentially jeopardizing the conservation of identity over long-time trajectories. The most advanced 3D tracking algorithms overcome optical occlusions making use of set-cover techniques, which however have to solve NP-hard optimization problems. Moreover, current methods are not able to cope with occlusions arising from actual physical proximity of objects in 3D space. Here, we present a new method designed to work directly in 3D space and time, creating (3D+1) clouds of points representing the full spatio-temporal evolution of the moving targets. We can then use a simple connected components labeling routine, which is linear in time, to solve optical occlusions, hence lowering from NP to P the complexity of the problem. Finally, we use normalized cut spectral clustering to tackle 3D physical proximity.

GReTA - a novel Global and Recursive Tracking Algorithm in three dimensions

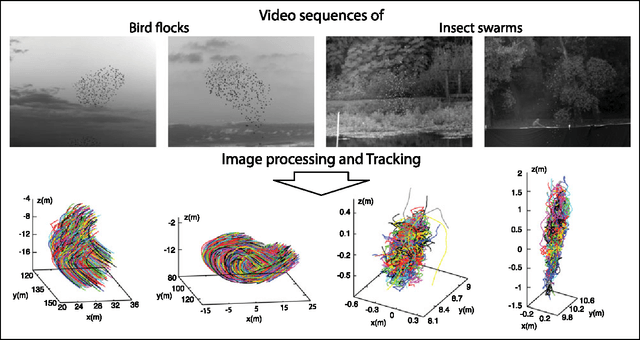
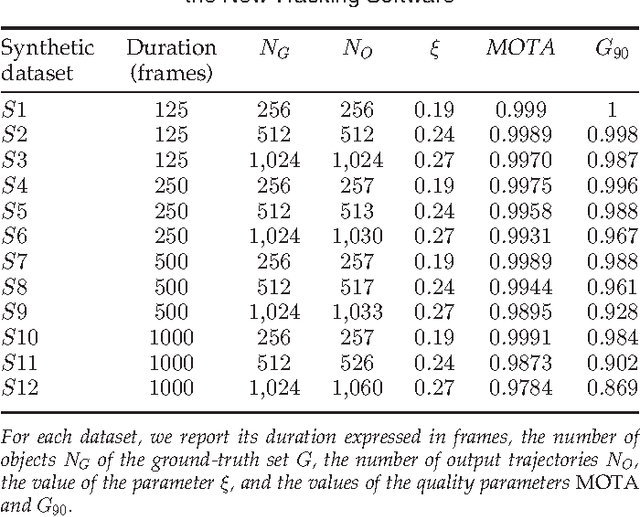
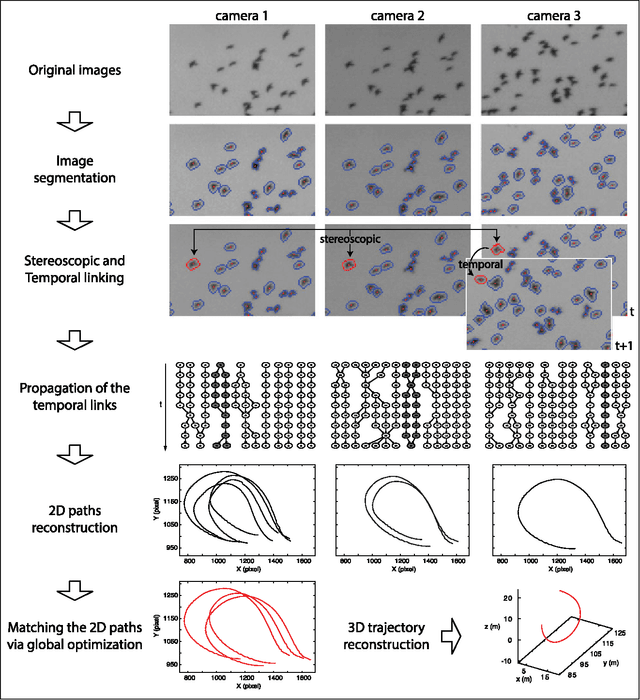
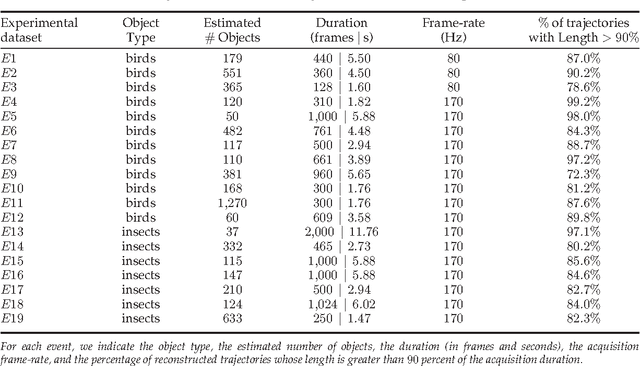
Tracking multiple moving targets allows quantitative measure of the dynamic behavior in systems as diverse as animal groups in biology, turbulence in fluid dynamics and crowd and traffic control. In three dimensions, tracking several targets becomes increasingly hard since optical occlusions are very likely, i.e. two featureless targets frequently overlap for several frames. Occlusions are particularly frequent in biological groups such as bird flocks, fish schools, and insect swarms, a fact that has severely limited collective animal behavior field studies in the past. This paper presents a 3D tracking method that is robust in the case of severe occlusions. To ensure robustness, we adopt a global optimization approach that works on all objects and frames at once. To achieve practicality and scalability, we employ a divide and conquer formulation, thanks to which the computational complexity of the problem is reduced by orders of magnitude. We tested our algorithm with synthetic data, with experimental data of bird flocks and insect swarms and with public benchmark datasets, and show that our system yields high quality trajectories for hundreds of moving targets with severe overlap. The results obtained on very heterogeneous data show the potential applicability of our method to the most diverse experimental situations.

Flocking and turning: a new model for self-organized collective motion

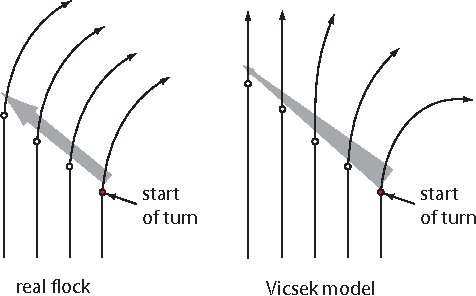
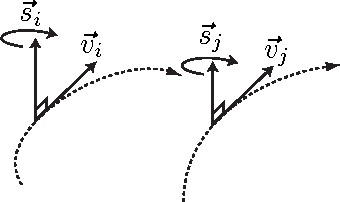
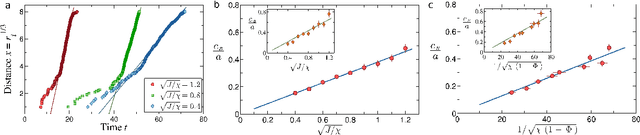
Birds in a flock move in a correlated way, resulting in large polarization of velocities. A good understanding of this collective behavior exists for linear motion of the flock. Yet observing actual birds, the center of mass of the group often turns giving rise to more complicated dynamics, still keeping strong polarization of the flock. Here we propose novel dynamical equations for the collective motion of polarized animal groups that account for correlated turning including solely social forces. We exploit rotational symmetries and conservation laws of the problem to formulate a theory in terms of generalized coordinates of motion for the velocity directions akin to a Hamiltonian formulation for rotations. We explicitly derive the correspondence between this formulation and the dynamics of the individual velocities, thus obtaining a new model of collective motion. In the appropriate overdamped limit we recover the well-known Vicsek model, which dissipates rotational information and does not allow for polarized turns. Although the new model has its most vivid success in describing turning groups, its dynamics is intrinsically different from previous ones in a wide dynamical regime, while reducing to the hydrodynamic description of Toner and Tu at very large length-scales. The derived framework is therefore general and it may describe the collective motion of any strongly polarized active matter system.