Safe Exploration for Constrained Reinforcement Learning with Provable Guarantees

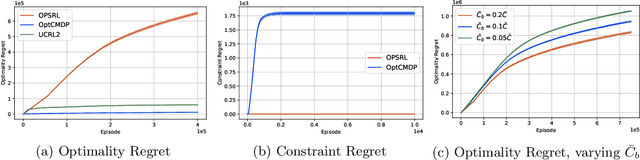
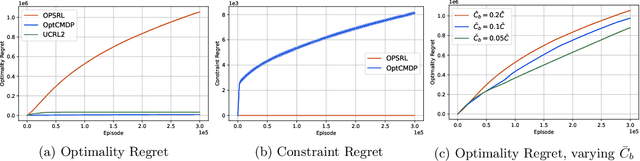
We consider the problem of learning an episodic safe control policy that minimizes an objective function, while satisfying necessary safety constraints -- both during learning and deployment. We formulate this safety constrained reinforcement learning (RL) problem using the framework of a finite-horizon Constrained Markov Decision Process (CMDP) with an unknown transition probability function. Here, we model the safety requirements as constraints on the expected cumulative costs that must be satisfied during all episodes of learning. We propose a model-based safe RL algorithm that we call the Optimistic-Pessimistic Safe Reinforcement Learning (OPSRL) algorithm, and show that it achieves an $\tilde{\mathcal{O}}(S^{2}\sqrt{A H^{7}K}/ (\bar{C} - \bar{C}_{b}))$ cumulative regret without violating the safety constraints during learning, where $S$ is the number of states, $A$ is the number of actions, $H$ is the horizon length, $K$ is the number of learning episodes, and $(\bar{C} - \bar{C}_{b})$ is the safety gap, i.e., the difference between the constraint value and the cost of a known safe baseline policy. The scaling as $\tilde{\mathcal{O}}(\sqrt{K})$ is the same as the traditional approach where constraints may be violated during learning, which means that our algorithm suffers no additional regret in spite of providing a safety guarantee. Our key idea is to use an optimistic exploration approach with pessimistic constraint enforcement for learning the policy. This approach simultaneously incentivizes the exploration of unknown states while imposing a penalty for visiting states that are likely to cause violation of safety constraints. We validate our algorithm by evaluating its performance on benchmark problems against conventional approaches.

Learning with Safety Constraints: Sample Complexity of Reinforcement Learning for Constrained MDPs

Many physical systems have underlying safety considerations that require that the policy employed ensures the satisfaction of a set of constraints. The analytical formulation usually takes the form of a Constrained Markov Decision Process (CMDP), where the constraints are some function of the occupancy measure generated by the policy. We focus on the case where the CMDP is unknown, and RL algorithms obtain samples to discover the model and compute an optimal constrained policy. Our goal is to characterize the relationship between safety constraints and the number of samples needed to ensure a desired level of accuracy---both objective maximization and constraint satisfaction---in a PAC sense. We explore generative model based class of RL algorithms wherein samples are taken initially to estimate a model. Our main finding is that compared to the best known bounds of the unconstrained regime, the sample complexity of constrained RL algorithms are increased by a factor that is logarithmic in the number of constraints, which suggests that the approach may be easily utilized in real systems.