Safe Exploration for Constrained Reinforcement Learning with Provable Guarantees
Paper and Code
Dec 01, 2021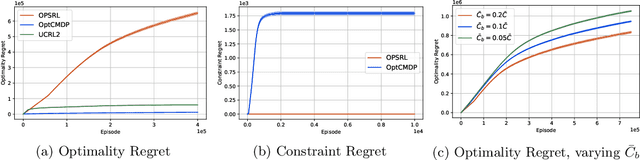
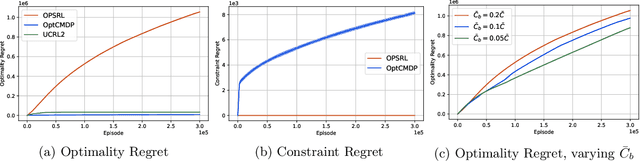
We consider the problem of learning an episodic safe control policy that minimizes an objective function, while satisfying necessary safety constraints -- both during learning and deployment. We formulate this safety constrained reinforcement learning (RL) problem using the framework of a finite-horizon Constrained Markov Decision Process (CMDP) with an unknown transition probability function. Here, we model the safety requirements as constraints on the expected cumulative costs that must be satisfied during all episodes of learning. We propose a model-based safe RL algorithm that we call the Optimistic-Pessimistic Safe Reinforcement Learning (OPSRL) algorithm, and show that it achieves an $\tilde{\mathcal{O}}(S^{2}\sqrt{A H^{7}K}/ (\bar{C} - \bar{C}_{b}))$ cumulative regret without violating the safety constraints during learning, where $S$ is the number of states, $A$ is the number of actions, $H$ is the horizon length, $K$ is the number of learning episodes, and $(\bar{C} - \bar{C}_{b})$ is the safety gap, i.e., the difference between the constraint value and the cost of a known safe baseline policy. The scaling as $\tilde{\mathcal{O}}(\sqrt{K})$ is the same as the traditional approach where constraints may be violated during learning, which means that our algorithm suffers no additional regret in spite of providing a safety guarantee. Our key idea is to use an optimistic exploration approach with pessimistic constraint enforcement for learning the policy. This approach simultaneously incentivizes the exploration of unknown states while imposing a penalty for visiting states that are likely to cause violation of safety constraints. We validate our algorithm by evaluating its performance on benchmark problems against conventional approaches.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge