Tensor Regression Networks

Convolutional neural networks typically consist of many convolutional layers followed by several fully-connected layers. While convolutional layers map between high-order activation tensors, the fully-connected layers operate on flattened activation vectors. Despite its success, this approach has notable drawbacks. Flattening discards multilinear structure in the activations, and fully-connected layers require many parameters. We address these problems by incorporating tensor algebraic operations that preserve multilinear structure at every layer. First, we introduce Tensor Contraction Layers (TCLs) that reduce the dimensionality of their input while preserving their multilinear structure using tensor contraction. Next, we introduce Tensor Regression Layers (TRLs), to express outputs through a low-rank multilinear mapping from a high-order activation tensor to an output tensor of arbitrary order. We learn the contraction and regression factors end-to-end, and by imposing low rank on both, we produce accurate nets with few parameters. Additionally, our layers regularize networks by imposing low-rank constraints on the activations (TCL) and regression weights (TRL). Experiments on ImageNet show that, applied to VGG and ResNet architectures, TCLs and TRLs reduce the number of parameters compared to fully-connected layers by more than 65% without impacting accuracy.

StrassenNets: Deep Learning with a Multiplication Budget

A large fraction of the arithmetic operations required to evaluate deep neural networks (DNNs) consists of matrix multiplications, in both convolution and fully connected layers. We perform end-to-end learning of low-cost approximations of matrix multiplications in DNN layers by casting matrix multiplications as 2-layer sum-product networks (SPNs) (arithmetic circuits) and learning their (ternary) edge weights from data. The SPNs disentangle multiplication and addition operations and enable us to impose a budget on the number of multiplication operations. Combining our method with knowledge distillation and applying it to image classification DNNs (trained on ImageNet) and language modeling DNNs (using LSTMs), we obtain a first-of-a-kind reduction in number of multiplications (over 99.5%) while maintaining the predictive performance of the full-precision models. Finally, we demonstrate that the proposed framework is able to rediscover Strassen's matrix multiplication algorithm, learning to multiply $2 \times 2$ matrices using only 7 multiplications instead of 8.

Stochastic Activation Pruning for Robust Adversarial Defense

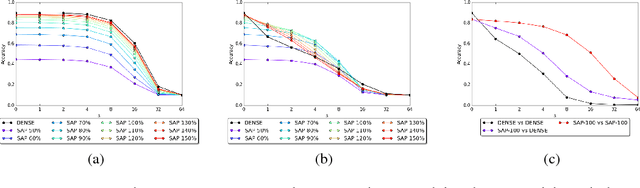
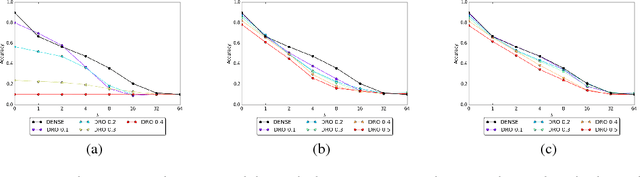
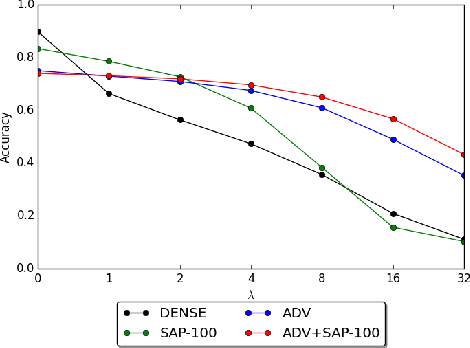
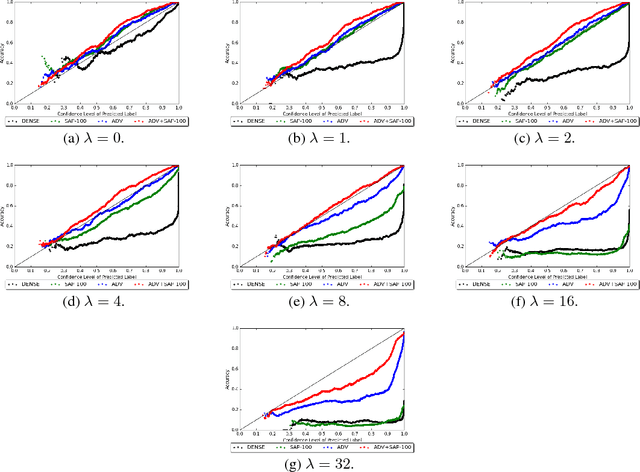
Neural networks are known to be vulnerable to adversarial examples. Carefully chosen perturbations to real images, while imperceptible to humans, induce misclassification and threaten the reliability of deep learning systems in the wild. To guard against adversarial examples, we take inspiration from game theory and cast the problem as a minimax zero-sum game between the adversary and the model. In general, for such games, the optimal strategy for both players requires a stochastic policy, also known as a mixed strategy. In this light, we propose Stochastic Activation Pruning (SAP), a mixed strategy for adversarial defense. SAP prunes a random subset of activations (preferentially pruning those with smaller magnitude) and scales up the survivors to compensate. We can apply SAP to pretrained networks, including adversarially trained models, without fine-tuning, providing robustness against adversarial examples. Experiments demonstrate that SAP confers robustness against attacks, increasing accuracy and preserving calibration.

Tensor Contraction Layers for Parsimonious Deep Nets

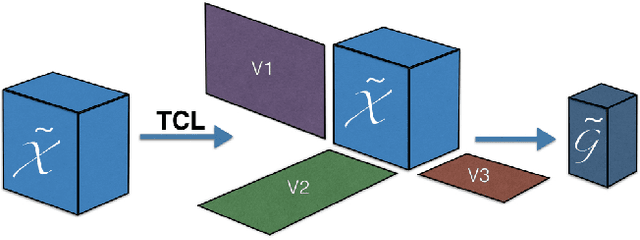
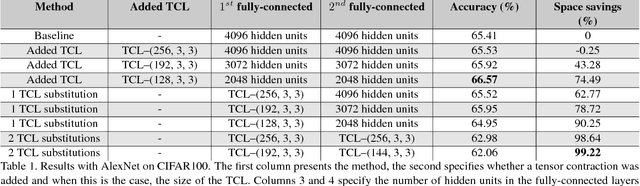
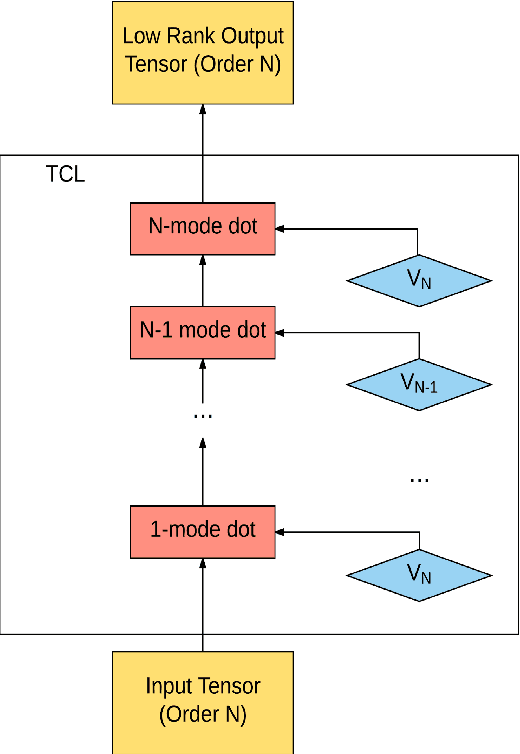
Tensors offer a natural representation for many kinds of data frequently encountered in machine learning. Images, for example, are naturally represented as third order tensors, where the modes correspond to height, width, and channels. Tensor methods are noted for their ability to discover multi-dimensional dependencies, and tensor decompositions in particular, have been used to produce compact low-rank approximations of data. In this paper, we explore the use of tensor contractions as neural network layers and investigate several ways to apply them to activation tensors. Specifically, we propose the Tensor Contraction Layer (TCL), the first attempt to incorporate tensor contractions as end-to-end trainable neural network layers. Applied to existing networks, TCLs reduce the dimensionality of the activation tensors and thus the number of model parameters. We evaluate the TCL on the task of image recognition, augmenting two popular networks (AlexNet, VGG). The resulting models are trainable end-to-end. Applying the TCL to the task of image recognition, using the CIFAR100 and ImageNet datasets, we evaluate the effect of parameter reduction via tensor contraction on performance. We demonstrate significant model compression without significant impact on the accuracy and, in some cases, improved performance.