Lossy Compression via Sparse Linear Regression: Performance under Minimum-distance Encoding

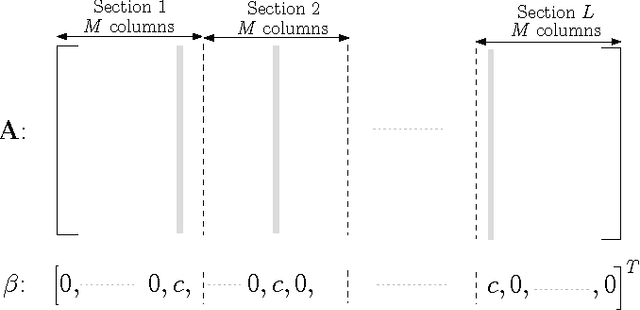
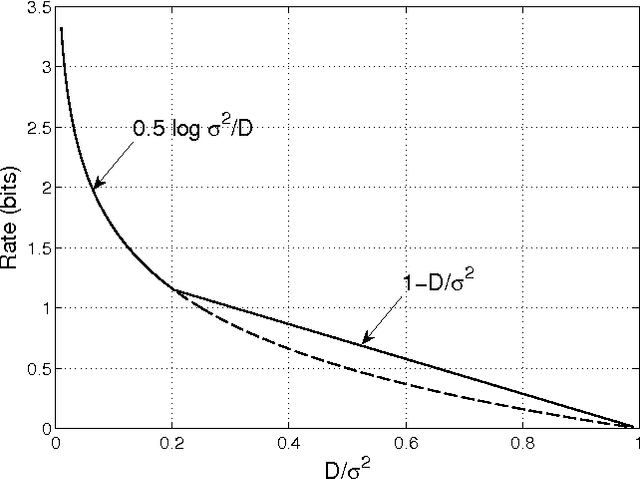
We study a new class of codes for lossy compression with the squared-error distortion criterion, designed using the statistical framework of high-dimensional linear regression. Codewords are linear combinations of subsets of columns of a design matrix. Called a Sparse Superposition or Sparse Regression codebook, this structure is motivated by an analogous construction proposed recently by Barron and Joseph for communication over an AWGN channel. For i.i.d Gaussian sources and minimum-distance encoding, we show that such a code can attain the Shannon rate-distortion function with the optimal error exponent, for all distortions below a specified value. It is also shown that sparse regression codes are robust in the following sense: a codebook designed to compress an i.i.d Gaussian source of variance $\sigma^2$ with (squared-error) distortion $D$ can compress any ergodic source of variance less than $\sigma^2$ to within distortion $D$. Thus the sparse regression ensemble retains many of the good covering properties of the i.i.d random Gaussian ensemble, while having having a compact representation in terms of a matrix whose size is a low-order polynomial in the block-length.

Impact of regularization on Spectral Clustering

The performance of spectral clustering can be considerably improved via regularization, as demonstrated empirically in Amini et. al (2012). Here, we provide an attempt at quantifying this improvement through theoretical analysis. Under the stochastic block model (SBM), and its extensions, previous results on spectral clustering relied on the minimum degree of the graph being sufficiently large for its good performance. By examining the scenario where the regularization parameter $\tau$ is large we show that the minimum degree assumption can potentially be removed. As a special case, for an SBM with two blocks, the results require the maximum degree to be large (grow faster than $\log n$) as opposed to the minimum degree. More importantly, we show the usefulness of regularization in situations where not all nodes belong to well-defined clusters. Our results rely on a `bias-variance'-like trade-off that arises from understanding the concentration of the sample Laplacian and the eigen gap as a function of the regularization parameter. As a byproduct of our bounds, we propose a data-driven technique \textit{DKest} (standing for estimated Davis-Kahan bounds) for choosing the regularization parameter. This technique is shown to work well through simulations and on a real data set.

Variable Selection in High Dimensions with Random Designs and Orthogonal Matching Pursuit

The performance of Orthogonal Matching Pursuit (OMP) for variable selection is analyzed for random designs. When contrasted with the deterministic case, since the performance is here measured after averaging over the distribution of the design matrix, one can have far less stringent sparsity constraints on the coefficient vector. We demonstrate that for exact sparse vectors, the performance of the OMP is similar to known results on the Lasso algorithm [\textit{IEEE Trans. Inform. Theory} \textbf{55} (2009) 2183--2202]. Moreover, variable selection under a more relaxed sparsity assumption on the coefficient vector, whereby one has only control on the $\ell_1$ norm of the smaller coefficients, is also analyzed. As a consequence of these results, we also show that the coefficient estimate satisfies strong oracle type inequalities.

Toward Fast Reliable Communication at Rates Near Capacity with Gaussian Noise

For the additive Gaussian noise channel with average codeword power constraint, sparse superposition codes and adaptive successive decoding is developed. Codewords are linear combinations of subsets of vectors, with the message indexed by the choice of subset. A feasible decoding algorithm is presented. Communication is reliable with error probability exponentially small for all rates below the Shannon capacity.

Least Squares Superposition Codes of Moderate Dictionary Size, Reliable at Rates up to Capacity

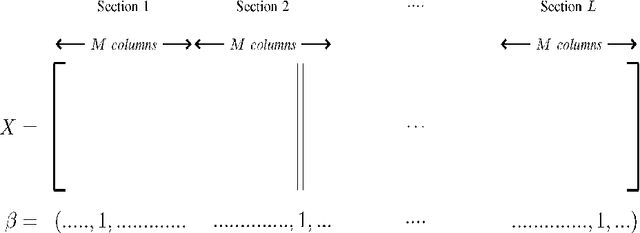
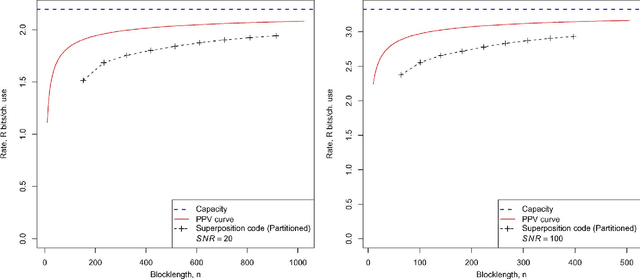
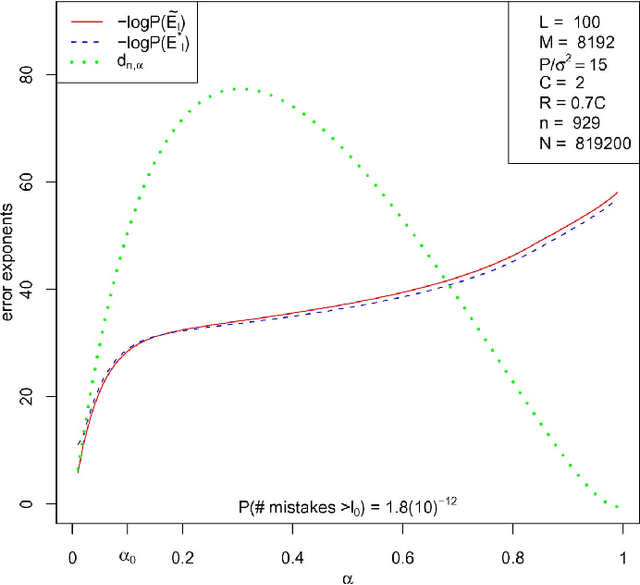
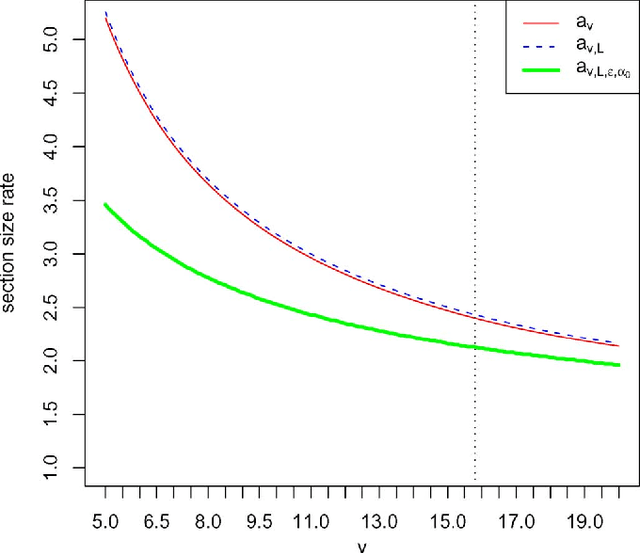
For the additive white Gaussian noise channel with average codeword power constraint, new coding methods are devised in which the codewords are sparse superpositions, that is, linear combinations of subsets of vectors from a given design, with the possible messages indexed by the choice of subset. Decoding is by least squares, tailored to the assumed form of linear combination. Communication is shown to be reliable with error probability exponentially small for all rates up to the Shannon capacity.