Improved MDL Estimators Using Fiber Bundle of Local Exponential Families for Non-exponential Families

Minimum Description Length (MDL) estimators, using two-part codes for universal coding, are analyzed. For general parametric families under certain regularity conditions, we introduce a two-part code whose regret is close to the minimax regret, where regret of a code with respect to a target family M is the difference between the code length of the code and the ideal code length achieved by an element in M. This is a generalization of the result for exponential families by Gr\"unwald. Our code is constructed by using an augmented structure of M with a bundle of local exponential families for data description, which is not needed for exponential families. This result gives a tight upper bound on risk and loss of the MDL estimators based on the theory introduced by Barron and Cover in 1991. Further, we show that we can apply the result to mixture families, which are a typical example of non-exponential families.

Complexity, Statistical Risk, and Metric Entropy of Deep Nets Using Total Path Variation

For any ReLU network there is a representation in which the sum of the absolute values of the weights into each node is exactly $1$, and the input layer variables are multiplied by a value $V$ coinciding with the total variation of the path weights. Implications are given for Gaussian complexity, Rademacher complexity, statistical risk, and metric entropy, all of which are shown to be proportional to $V$. There is no dependence on the number of nodes per layer, except for the number of inputs $d$. For estimation with sub-Gaussian noise, the mean square generalization error bounds that can be obtained are of order $V \sqrt{L + \log d}/\sqrt{n}$, where $L$ is the number of layers and $n$ is the sample size.

Risk Bounds for High-dimensional Ridge Function Combinations Including Neural Networks

Let $ f^{\star} $ be a function on $ \mathbb{R}^d $ with an assumption of a spectral norm $ v_{f^{\star}} $. For various noise settings, we show that $ \mathbb{E}\|\hat{f} - f^{\star} \|^2 \leq \left(v^4_{f^{\star}}\frac{\log d}{n}\right)^{1/3} $, where $ n $ is the sample size and $ \hat{f} $ is either a penalized least squares estimator or a greedily obtained version of such using linear combinations of sinusoidal, sigmoidal, ramp, ramp-squared or other smooth ridge functions. The candidate fits may be chosen from a continuum of functions, thus avoiding the rigidity of discretizations of the parameter space. On the other hand, if the candidate fits are chosen from a discretization, we show that $ \mathbb{E}\|\hat{f} - f^{\star} \|^2 \leq \left(v^3_{f^{\star}}\frac{\log d}{n}\right)^{2/5} $. This work bridges non-linear and non-parametric function estimation and includes single-hidden layer nets. Unlike past theory for such settings, our bound shows that the risk is small even when the input dimension $ d $ of an infinite-dimensional parameterized dictionary is much larger than the available sample size. When the dimension is larger than the cube root of the sample size, this quantity is seen to improve the more familiar risk bound of $ v_{f^{\star}}\left(\frac{d\log (n/d)}{n}\right)^{1/2} $, also investigated here.

Approximation and Estimation for High-Dimensional Deep Learning Networks

It has been experimentally observed in recent years that multi-layer artificial neural networks have a surprising ability to generalize, even when trained with far more parameters than observations. Is there a theoretical basis for this? The best available bounds on their metric entropy and associated complexity measures are essentially linear in the number of parameters, which is inadequate to explain this phenomenon. Here we examine the statistical risk (mean squared predictive error) of multi-layer networks with $\ell^1$-type controls on their parameters and with ramp activation functions (also called lower-rectified linear units). In this setting, the risk is shown to be upper bounded by $[(L^3 \log d)/n]^{1/2}$, where $d$ is the input dimension to each layer, $L$ is the number of layers, and $n$ is the sample size. In this way, the input dimension can be much larger than the sample size and the estimator can still be accurate, provided the target function has such $\ell^1$ controls and that the sample size is at least moderately large compared to $L^3\log d$. The heart of the analysis is the development of a sampling strategy that demonstrates the accuracy of a sparse covering of deep ramp networks. Lower bounds show that the identified risk is close to being optimal.

Approximation by Combinations of ReLU and Squared ReLU Ridge Functions with $ \ell^1 $ and $ \ell^0 $ Controls

We establish $ L^{\infty} $ and $ L^2 $ error bounds for functions of many variables that are approximated by linear combinations of ReLU (rectified linear unit) and squared ReLU ridge functions with $ \ell^1 $ and $ \ell^0 $ controls on their inner and outer parameters. With the squared ReLU ridge function, we show that the $ L^2 $ approximation error is inversely proportional to the inner layer $ \ell^0 $ sparsity and it need only be sublinear in the outer layer $ \ell^0 $ sparsity. Our constructions are obtained using a variant of the Jones-Barron probabilistic method, which can be interpreted as either stratified sampling with proportionate allocation or two-stage cluster sampling. We also provide companion error lower bounds that reveal near optimality of our constructions. Despite the sparsity assumptions, we showcase the richness and flexibility of these ridge combinations by defining a large family of functions, in terms of certain spectral conditions, that are particularly well approximated by them.

Minimax Lower Bounds for Ridge Combinations Including Neural Nets

Estimation of functions of $ d $ variables is considered using ridge combinations of the form $ \textstyle\sum_{k=1}^m c_{1,k} \phi(\textstyle\sum_{j=1}^d c_{0,j,k}x_j-b_k) $ where the activation function $ \phi $ is a function with bounded value and derivative. These include single-hidden layer neural networks, polynomials, and sinusoidal models. From a sample of size $ n $ of possibly noisy values at random sites $ X \in B = [-1,1]^d $, the minimax mean square error is examined for functions in the closure of the $ \ell_1 $ hull of ridge functions with activation $ \phi $. It is shown to be of order $ d/n $ to a fractional power (when $ d $ is of smaller order than $ n $), and to be of order $ (\log d)/n $ to a fractional power (when $ d $ is of larger order than $ n $). Dependence on constraints $ v_0 $ and $ v_1 $ on the $ \ell_1 $ norms of inner parameter $ c_0 $ and outer parameter $ c_1 $, respectively, is also examined. Also, lower and upper bounds on the fractional power are given. The heart of the analysis is development of information-theoretic packing numbers for these classes of functions.

Least Squares Superposition Codes of Moderate Dictionary Size, Reliable at Rates up to Capacity

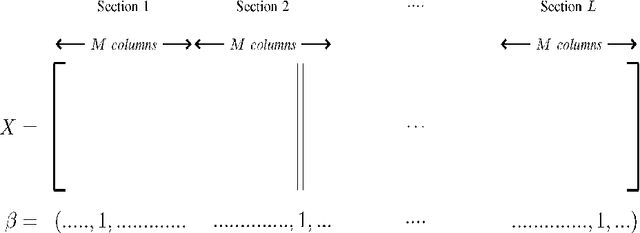
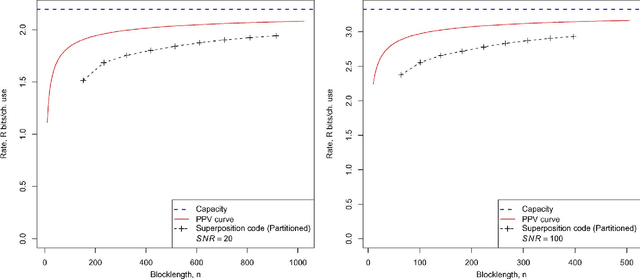
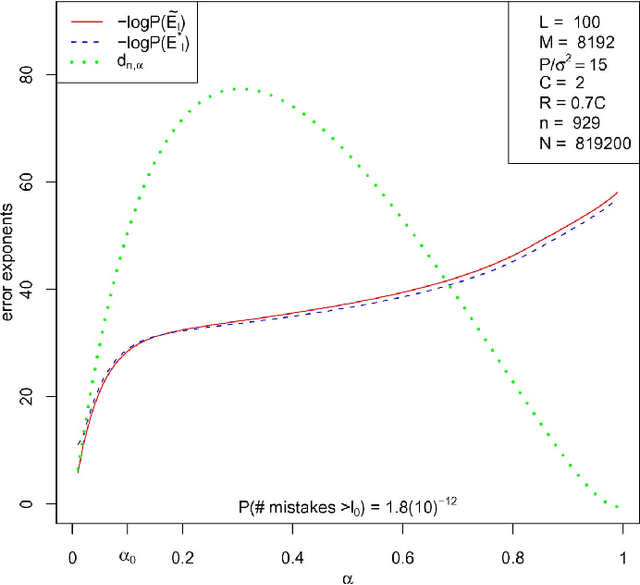
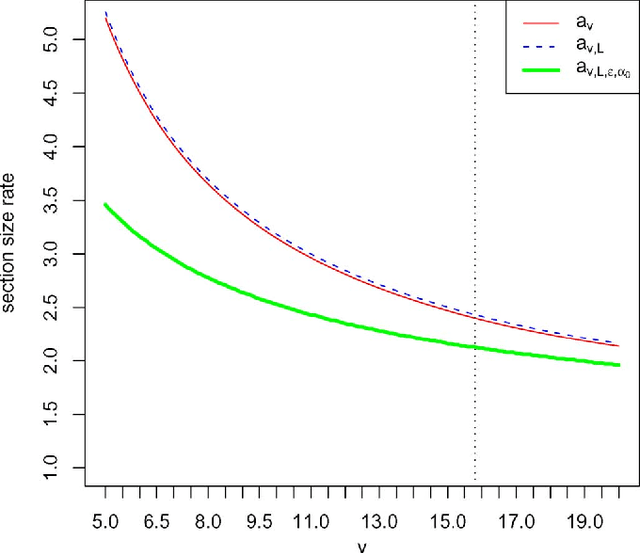
For the additive white Gaussian noise channel with average codeword power constraint, new coding methods are devised in which the codewords are sparse superpositions, that is, linear combinations of subsets of vectors from a given design, with the possible messages indexed by the choice of subset. Decoding is by least squares, tailored to the assumed form of linear combination. Communication is shown to be reliable with error probability exponentially small for all rates up to the Shannon capacity.