Gamified and Self-Adaptive Applications for the Common Good: Research Challenges Ahead

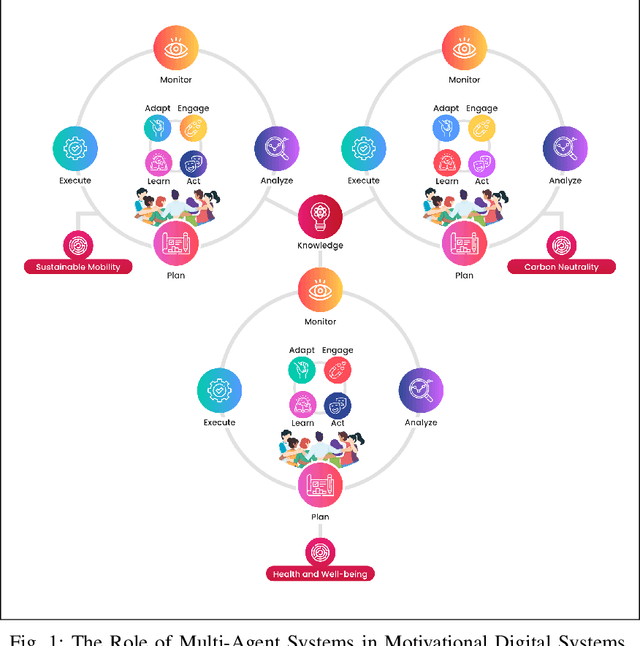
Motivational digital systems offer capabilities to engage and motivate end-users to foster behavioral changes towards a common goal. In general these systems use gamification principles in non-games contexts. Over the years, gamification has gained consensus among researchers and practitioners as a tool to motivate people to perform activities with the ultimate goal of promoting behavioural change, or engaging the users to perform activities that can offer relevant benefits but which can be seen as unrewarding and even tedious. There exists a plethora of heterogeneous application scenarios towards reaching the common good that can benefit from gamification. However, an open problem is how to effectively combine multiple motivational campaigns to maximise the degree of participation without exposing the system to counterproductive behaviours. We conceive motivational digital systems as multi-agent systems: self-adaptation is a feature of the overall system, while individual agents may self-adapt in order to leverage other agents' resources, functionalities and capabilities to perform tasks more efficiently and effectively. Consequently, multiple campaigns can be run and adapted to reach common good. At the same time, agents are grouped into micro-communities in which agents contribute with their own social capital and leverage others' capabilities to balance their weaknesses. In this paper we propose our vision on how the principles at the base of the autonomous and multi-agent systems can be exploited to design multi-challenge motivational systems to engage smart communities towards common goals. We present an initial version of a general framework based on the MAPE-K loop and a set of research challenges that characterise our research roadmap for the implementation of our vision.

Learning Neural Search Policies for Classical Planning

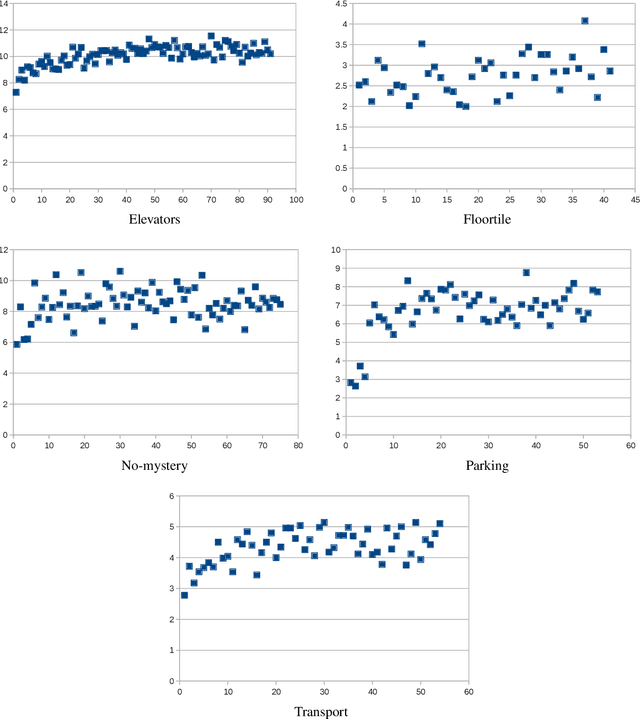
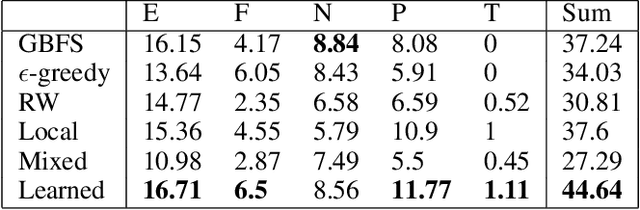
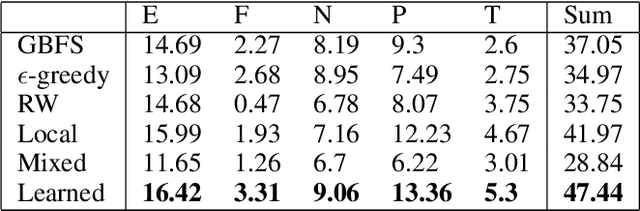
Heuristic forward search is currently the dominant paradigm in classical planning. Forward search algorithms typically rely on a single, relatively simple variation of best-first search and remain fixed throughout the process of solving a planning problem. Existing work combining multiple search techniques usually aims at supporting best-first search with an additional exploratory mechanism, triggered using a handcrafted criterion. A notable exception is very recent work which combines various search techniques using a trainable policy. It is, however, confined to a discrete action space comprising several fixed subroutines. In this paper, we introduce a parametrized search algorithm template which combines various search techniques within a single routine. The template's parameter space defines an infinite space of search algorithms, including, among others, BFS, local and random search. We further introduce a neural architecture for designating the values of the search parameters given the state of the search. This enables expressing neural search policies that change the values of the parameters as the search progresses. The policies can be learned automatically, with the objective of maximizing the planner's performance on a given distribution of planning problems. We consider a training setting based on a stochastic optimization algorithm known as the cross-entropy method (CEM). Experimental evaluation of our approach shows that it is capable of finding effective distribution-specific search policies, outperforming the relevant baselines.

Towards learning domain-independent planning heuristics

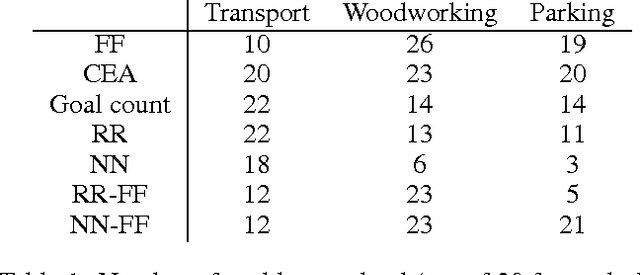
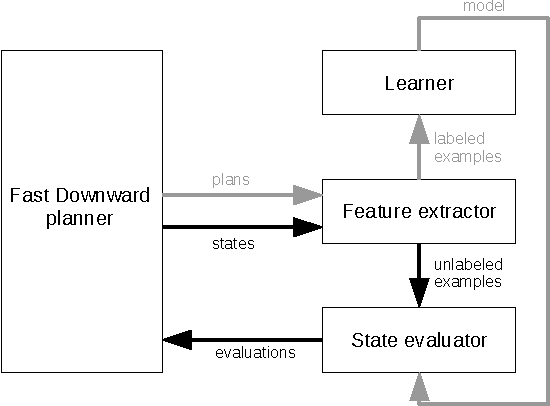
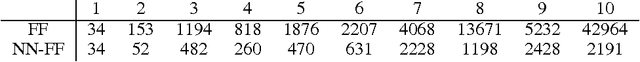
Automated planning remains one of the most general paradigms in Artificial Intelligence, providing means of solving problems coming from a wide variety of domains. One of the key factors restricting the applicability of planning is its computational complexity resulting from exponentially large search spaces. Heuristic approaches are necessary to solve all but the simplest problems. In this work, we explore the possibility of obtaining domain-independent heuristic functions using machine learning. This is a part of a wider research program whose objective is to improve practical applicability of planning in systems for which the planning domains evolve at run time. The challenge is therefore the learning of (corrections of) domain-independent heuristics that can be reused across different planning domains.