Learning Neural Search Policies for Classical Planning

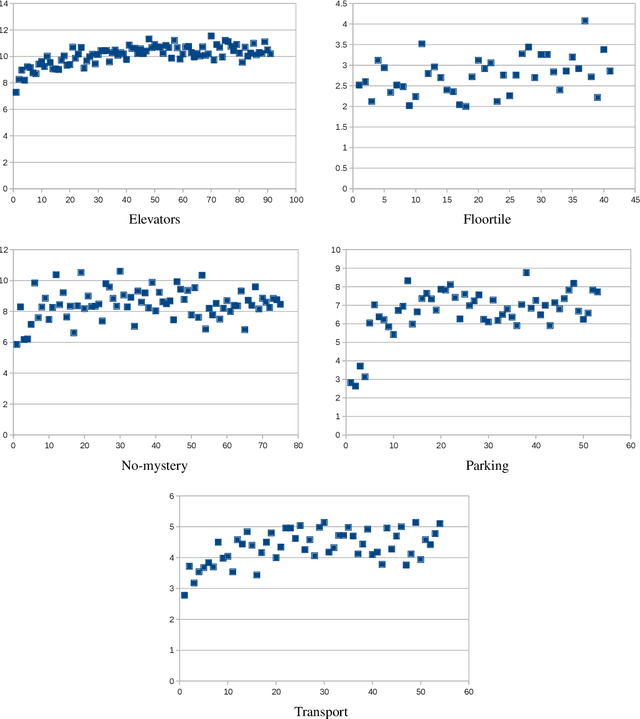
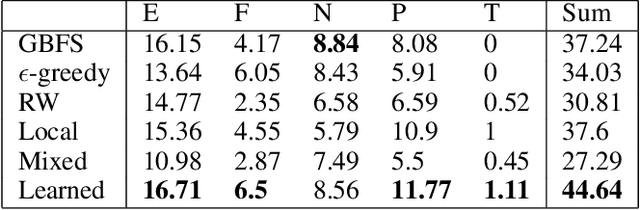
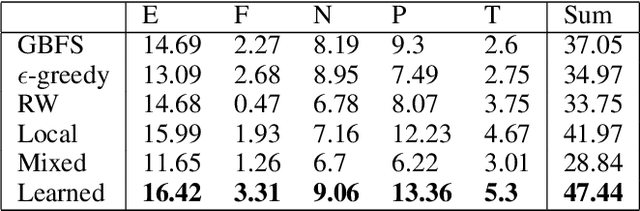
Heuristic forward search is currently the dominant paradigm in classical planning. Forward search algorithms typically rely on a single, relatively simple variation of best-first search and remain fixed throughout the process of solving a planning problem. Existing work combining multiple search techniques usually aims at supporting best-first search with an additional exploratory mechanism, triggered using a handcrafted criterion. A notable exception is very recent work which combines various search techniques using a trainable policy. It is, however, confined to a discrete action space comprising several fixed subroutines. In this paper, we introduce a parametrized search algorithm template which combines various search techniques within a single routine. The template's parameter space defines an infinite space of search algorithms, including, among others, BFS, local and random search. We further introduce a neural architecture for designating the values of the search parameters given the state of the search. This enables expressing neural search policies that change the values of the parameters as the search progresses. The policies can be learned automatically, with the objective of maximizing the planner's performance on a given distribution of planning problems. We consider a training setting based on a stochastic optimization algorithm known as the cross-entropy method (CEM). Experimental evaluation of our approach shows that it is capable of finding effective distribution-specific search policies, outperforming the relevant baselines.

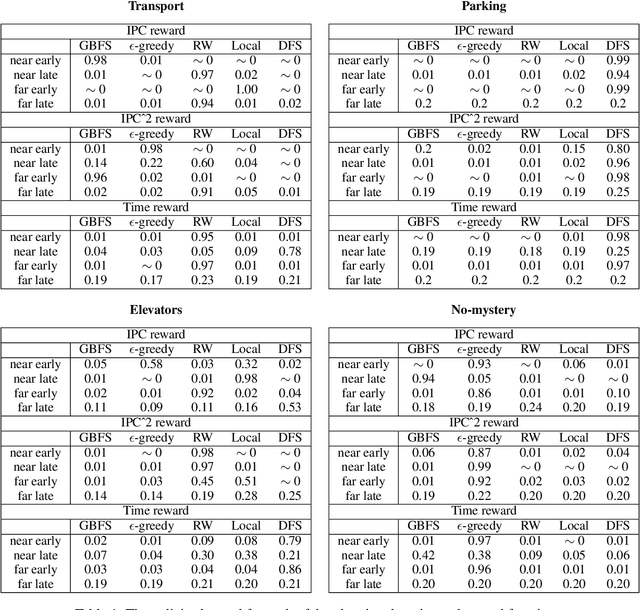
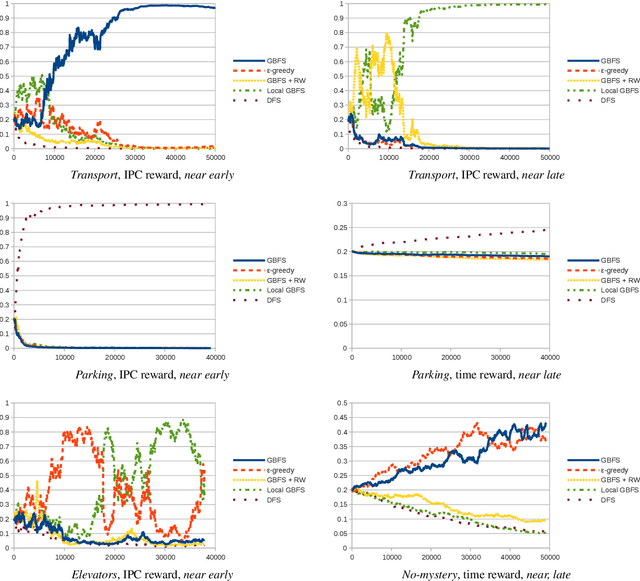
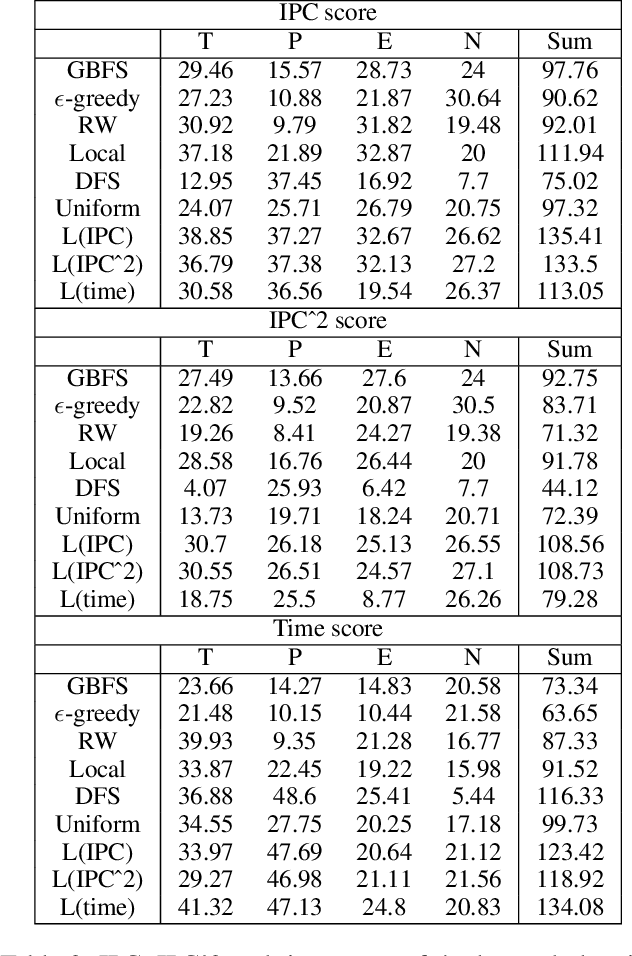
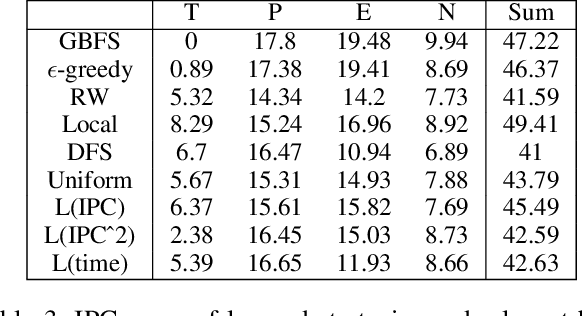
Learning Classical Planning Strategies with Policy Gradient

A common paradigm in classical planning is heuristic forward search. Forward search planners often rely on relatively simple best-first search algorithm, which remains fixed throughout the search process. In this paper, we introduce a novel search framework capable of alternating between several forward search approaches while solving a particular planning problem. Selection of the approach is performed using a trainable stochastic policy. This enables tailoring the search strategy to a particular distribution of planning problems and a selected performance metric, such as the IPC score or running time. We construct a strategy space using five search algorithms and a two-dimensional representation of the planner's state. Strategies are then trained on randomly generated planning problems using policy gradient. Experimental results show that the learner is able to discover domain-specific search strategies, thus improving the planner's performance with respect to the chosen metric.

Towards learning domain-independent planning heuristics

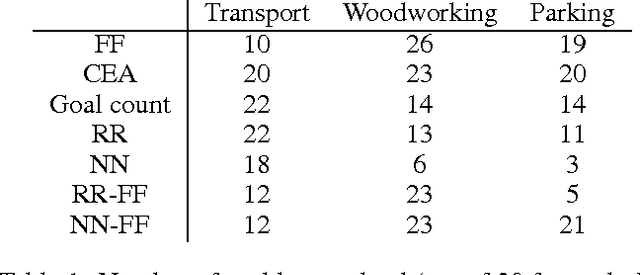
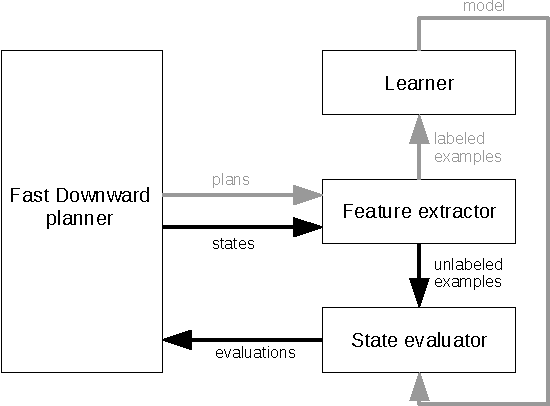
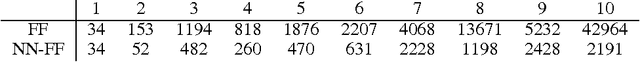
Automated planning remains one of the most general paradigms in Artificial Intelligence, providing means of solving problems coming from a wide variety of domains. One of the key factors restricting the applicability of planning is its computational complexity resulting from exponentially large search spaces. Heuristic approaches are necessary to solve all but the simplest problems. In this work, we explore the possibility of obtaining domain-independent heuristic functions using machine learning. This is a part of a wider research program whose objective is to improve practical applicability of planning in systems for which the planning domains evolve at run time. The challenge is therefore the learning of (corrections of) domain-independent heuristics that can be reused across different planning domains.