Structure based SAT dataset for analysing GNN generalisation

Satisfiability (SAT) solvers based on techniques such as conflict driven clause learning (CDCL) have produced excellent performance on both synthetic and real world industrial problems. While these CDCL solvers only operate on a per-problem basis, graph neural network (GNN) based solvers bring new benefits to the field by allowing practitioners to exploit knowledge gained from solved problems to expedite solving of new SAT problems. However, one specific area that is often studied in the context of CDCL solvers, but largely overlooked in GNN solvers, is the relationship between graph theoretic measure of structure in SAT problems and the generalisation ability of GNN solvers. To bridge the gap between structural graph properties (e.g., modularity, self-similarity) and the generalisability (or lack thereof) of GNN based SAT solvers, we present StructureSAT: a curated dataset, along with code to further generate novel examples, containing a diverse set of SAT problems from well known problem domains. Furthermore, we utilise a novel splitting method that focuses on deconstructing the families into more detailed hierarchies based on their structural properties. With the new dataset, we aim to help explain problematic generalisation in existing GNN SAT solvers by exploiting knowledge of structural graph properties. We conclude with multiple future directions that can help researchers in GNN based SAT solving develop more effective and generalisable SAT solvers.

Sparse Spectrum Warped Input Measures for Nonstationary Kernel Learning

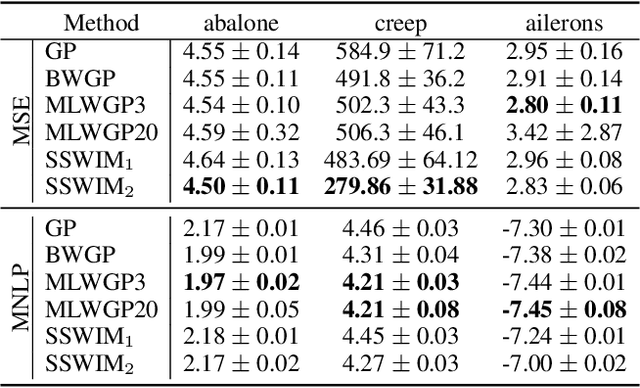
We establish a general form of explicit, input-dependent, measure-valued warpings for learning nonstationary kernels. While stationary kernels are ubiquitous and simple to use, they struggle to adapt to functions that vary in smoothness with respect to the input. The proposed learning algorithm warps inputs as conditional Gaussian measures that control the smoothness of a standard stationary kernel. This construction allows us to capture non-stationary patterns in the data and provides intuitive inductive bias. The resulting method is based on sparse spectrum Gaussian processes, enabling closed-form solutions, and is extensible to a stacked construction to capture more complex patterns. The method is extensively validated alongside related algorithms on synthetic and real world datasets. We demonstrate a remarkable efficiency in the number of parameters of the warping functions in learning problems with both small and large data regimes.

Online Domain Adaptation for Occupancy Mapping

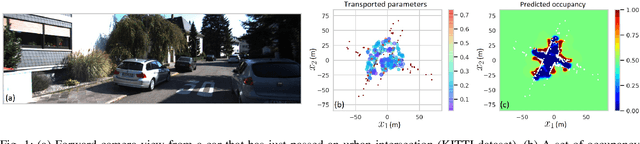
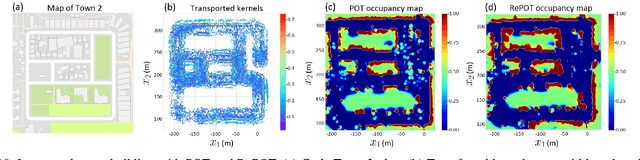
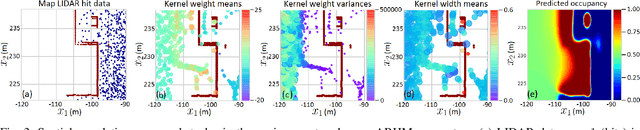
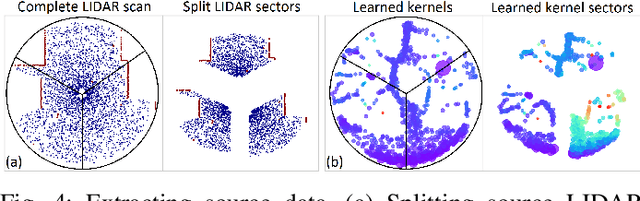
Creating accurate spatial representations that take into account uncertainty is critical for autonomous robots to safely navigate in unstructured environments. Although recent LIDAR based mapping techniques can produce robust occupancy maps, learning the parameters of such models demand considerable computational time, discouraging them from being used in real-time and large-scale applications such as autonomous driving. Recognizing the fact that real-world structures exhibit similar geometric features across a variety of urban environments, in this paper, we argue that it is redundant to learn all geometry dependent parameters from scratch. Instead, we propose a theoretical framework building upon the theory of optimal transport to adapt model parameters to account for changes in the environment, significantly amortizing the training cost. Further, with the use of high-fidelity driving simulators and real-world datasets, we demonstrate how parameters of 2D and 3D occupancy maps can be automatically adapted to accord with local spatial changes. We validate various domain adaptation paradigms through a series of experiments, ranging from inter-domain feature transfer to simulation-to-real-world feature transfer. Experiments verified the possibility of estimating parameters with a negligible computational and memory cost, enabling large-scale probabilistic mapping in urban environments.

Index Set Fourier Series Features for Approximating Multi-dimensional Periodic Kernels

Periodicity is often studied in timeseries modelling with autoregressive methods but is less popular in the kernel literature, particularly for higher dimensional problems such as in textures, crystallography, and quantum mechanics. Large datasets often make modelling periodicity untenable for otherwise powerful non-parametric methods like Gaussian Processes (GPs) which typically incur an $\mathcal{O}(N^3)$ computational burden and, consequently, are unable to scale to larger datasets. To this end we introduce a method termed \emph{Index Set Fourier Series Features} to tractably exploit multivariate Fourier series and efficiently decompose periodic kernels on higher-dimensional data into a series of basis functions. We show that our approximation produces significantly less predictive error than alternative approaches such as those based on random Fourier features and achieves better generalisation on regression problems with periodic data.