Comparative Analysis of Differential and Collision Entropy for Finite-Regime QKD in Hybrid Quantum Noisy Channels

In this work, a comparative study between three fundamental entropic measures, differential entropy, quantum Renyi entropy, and quantum collision entropy for a hybrid quantum channel (HQC) was investigated, where hybrid quantum noise (HQN) is characterized by both discrete and continuous variables (CV) noise components. Using a Gaussian mixture model (GMM) to statistically model the HQN, we construct as well as visualize the corresponding pointwise entropic functions in a given 3D probabilistic landscape. When integrated over the relevant state space, these entropic surfaces yield values of the respective global entropy. Through analytical and numerical evaluation, it is demonstrated that the differential entropy approaches the quantum collision entropy under certain mixing conditions, which aligns with the Renyi entropy for order $α= 2$. Within the HQC framework, the results establish a theoretical and computational equivalence between these measures. This provides a unified perspective on quantifying uncertainty in hybrid quantum communication systems. Extending the analysis to the operational domain of finite key QKD, we demonstrated that the same $10\%$ approximation threshold corresponds to an order-of-magnitude change in Eves success probability and a measurable reduction in the secure key rate.

Grover's Search-Inspired Quantum Reinforcement Learning for Massive MIMO User Scheduling

The efficient user scheduling policy in the massive Multiple Input Multiple Output (mMIMO) system remains a significant challenge in the field of 5G and Beyond 5G (B5G) due to its high computational complexity, scalability, and Channel State Information (CSI) overhead. This paper proposes a novel Grover's search-inspired Quantum Reinforcement Learning (QRL) framework for mMIMO user scheduling. The QRL agent can explore the exponentially large scheduling space effectively by applying Grover's search to the reinforcement learning process. The model is implemented using our designed quantum-gate-based circuit, which imitates the layered architecture of reinforcement learning, where quantum operations act as policy updates and decision-making units. Moreover, the simulation results demonstrate that the proposed method achieves proper convergence and significantly outperforms classical Convolutional Neural Networks (CNN) and Quantum Deep Learning (QDL) benchmarks.

On the Achievable Rate of Satellite Quantum Communication Channel using Deep Autoencoder Gaussian Mixture Model

We present a comparative study of the Gaussian mixture model (GMM) and the Deep Autoencoder Gaussian Mixture Model (DAGMM) for estimating satellite quantum channel capacity, considering hybrid quantum noise (HQN) and transmission constraints. While GMM is simple and interpretable, DAGMM better captures non-linear variations and noise distributions. Simulations show that DAGMM provides tighter capacity bounds and improved clustering. This introduces the Deep Cluster Gaussian Mixture Model (DCGMM) for high-dimensional quantum data analysis in quantum satellite communication.

A Hybrid Noise Approach to Modelling of Free-Space Satellite Quantum Communication Channel for Continuous-Variable QKD

This paper significantly advances the application of Quantum Key Distribution (QKD) in Free- Space Optics (FSO) satellite-based quantum communication. We propose an innovative satellite quantum channel model and derive the secret quantum key distribution rate achievable through this channel. Unlike existing models that approximate the noise in quantum channels as merely Gaussian distributed, our model incorporates a hybrid noise analysis, accounting for both quantum Poissonian noise and classical Additive-White-Gaussian Noise (AWGN). This hybrid approach acknowledges the dual vulnerability of continuous variables (CV) Gaussian quantum channels to both quantum and classical noise, thereby offering a more realistic assessment of the quantum Secret Key Rate (SKR). This paper delves into the variation of SKR with the Signal-to-Noise Ratio (SNR) under various influencing parameters. We identify and analyze critical factors such as reconciliation efficiency, transmission coefficient, transmission efficiency, the quantum Poissonian noise parameter, and the satellite altitude. These parameters are pivotal in determining the SKR in FSO satellite quantum channels, highlighting the challenges of satellitebased quantum communication. Our work provides a comprehensive framework for understanding and optimizing SKR in satellite-based QKD systems, paving the way for more efficient and secure quantum communication networks.

Hybrid Quantum Noise Approximation and Pattern Analysis on Parameterized Component Distributions

Noise is a vital factor in determining the accuracy of processing the information of the quantum channel. One must consider classical noise effects associated with quantum noise sources for more realistic modelling of quantum channels. A hybrid quantum noise model incorporating both quantum Poisson noise and classical additive white Gaussian noise (AWGN) can be interpreted as an infinite mixture of Gaussians with weightage from the Poisson distribution. The entropy measure of this function is difficult to calculate. This research developed how the infinite mixture can be well approximated by a finite mixture distribution depending on the Poisson parametric setting compared to the number of mixture components. The mathematical analysis of the characterization of hybrid quantum noise has been demonstrated based on Gaussian and Poisson parametric analysis. This helps in the pattern analysis of the parametric values of the component distribution, and it also helps in the calculation of hybrid noise entropy to understand hybrid quantum noise better.

A Machine Learning Approach for Optimizing Hybrid Quantum Noise Clusters for Gaussian Quantum Channel Capacity

This work contributes to the advancement of quantum communication by visualizing hybrid quantum noise in higher dimensions and optimizing the capacity of the quantum channel by using machine learning (ML). Employing the expectation maximization (EM) algorithm, the quantum channel parameters are iteratively adjusted to estimate the channel capacity, facilitating the categorization of quantum noise data in higher dimensions into a finite number of clusters. In contrast to previous investigations that represented the model in lower dimensions, our work describes the quantum noise as a Gaussian Mixture Model (GMM) with mixing weights derived from a Poisson distribution. The objective was to model the quantum noise using a finite mixture of Gaussian components while preserving the mixing coefficients from the Poisson distribution. Approximating the infinite Gaussian mixture with a finite number of components makes it feasible to visualize clusters of quantum noise data without modifying the original probability density function. By implementing the EM algorithm, the research fine-tuned the channel parameters, identified optimal clusters, improved channel capacity estimation, and offered insights into the characteristics of quantum noise within an ML framework.

On the Energy-Efficiency Maximization for IRS-Assisted MIMOME Wiretap Channels

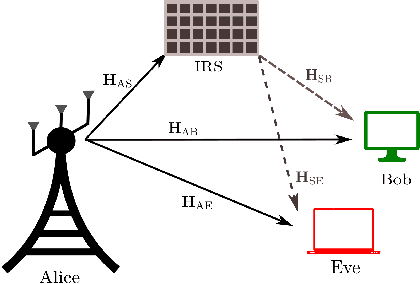
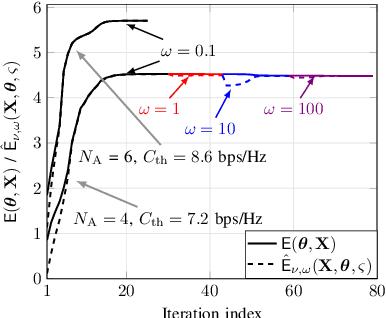
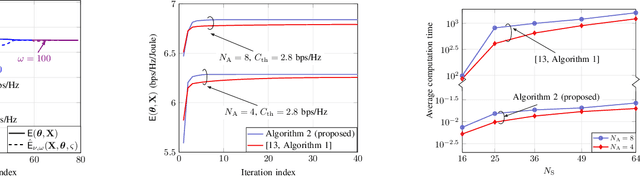
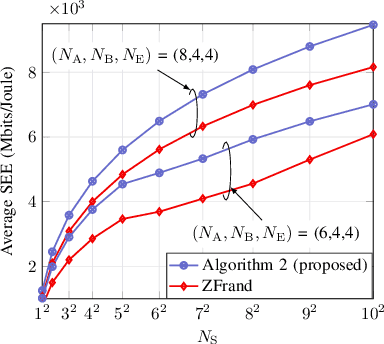
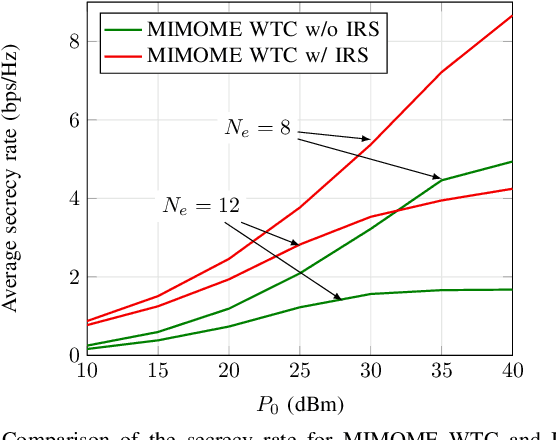
Security and energy efficiency have become crucial features in the modern-era wireless communication. In this paper, we consider an energy-efficient design for intelligent reflecting surface (IRS)-assisted multiple-input multiple-output multiple-eavesdropper (MIMOME) wiretap channels (WTC). Our objective is to jointly optimize the transmit covariance matrix and the IRS phase-shifts to maximize the secrecy energy efficiency (SEE) of the considered system subject to a secrecy rate constraint at the legitimate receiver. To tackle this challenging non-convex problem in which the design variables are coupled in the objective and the constraint, we propose a penalty dual decomposition based alternating gradient projection (PDDAPG) method to obtain an efficient solution. We also show that the computational complexity of the proposed algorithm grows only linearly with the number of reflecting elements at the IRS, as well as with the number of antennas at transmitter/receivers' nodes. Our results confirm that using an IRS is helpful to improve the SEE of MIMOME WTC compared to its no-IRS counterpart only when the power consumption at IRS is small. In particular, and a large-sized IRS is not always beneficial for the SEE of a MIMOME WTC.

Secrecy Rate Maximization for Intelligent Reflecting Surface Assisted MIMOME Wiretap Channels

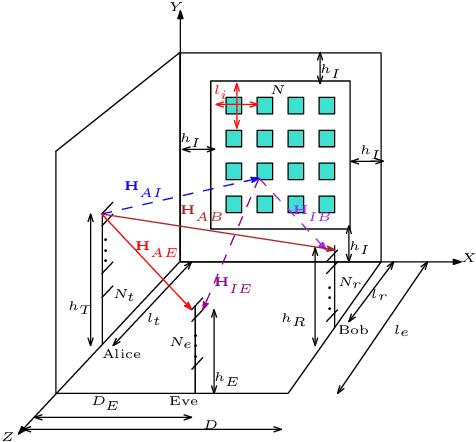
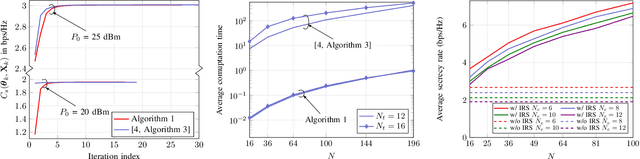
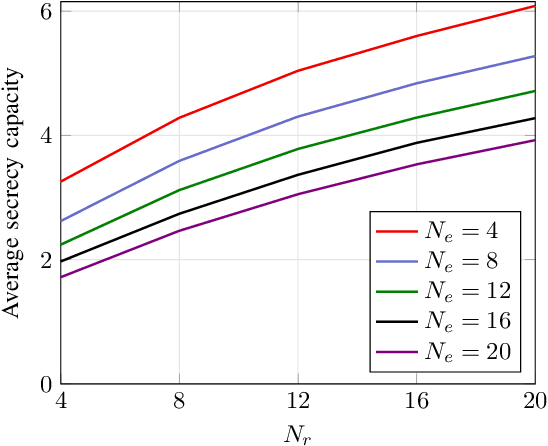
Intelligent reflecting surface (IRS) has gained tremendous attention recently as a disruptive technology for beyond 5G networks. In this paper, we consider the problem of secrecy rate maximization for an IRS-assisted Gaussian multiple-input multiple-output multi-antenna-eavesdropper (MIMOME) wiretap channel (WTC). In this context, we aim to jointly optimize the input covariance matrix and the IRS phase shifts to maximize the achievable secrecy rate of the considered system. To solve the formulated problem which is non-convex, we propose an iterative method based on the block successive maximization (BSM), where each iteration is done in closed form. More specifically, we maximize a lower bound on the achievable secrecy rate to update the input covariance matrix for fixed phase shifts, and then maximize the (exact) achievable secrecy rate to update phase shifts for a given input covariance.We consider the total free space path loss (FSPL) in this system to emphasize the first-order measure of the applicability of the IRS in the considered communication system. We present a convergence proof and the associated complexity analysis of the proposed algorithm. Numerical results are provided to demonstrate the superiority of the proposed method compared to a known solution, and also to show the effect of different parameters of interest on the achievable secrecy rate of the IRS-assisted MIMOME WTC.

On the Optimality of the Stationary Solution of Secrecy Rate Maximization for MIMO Wiretap Channel

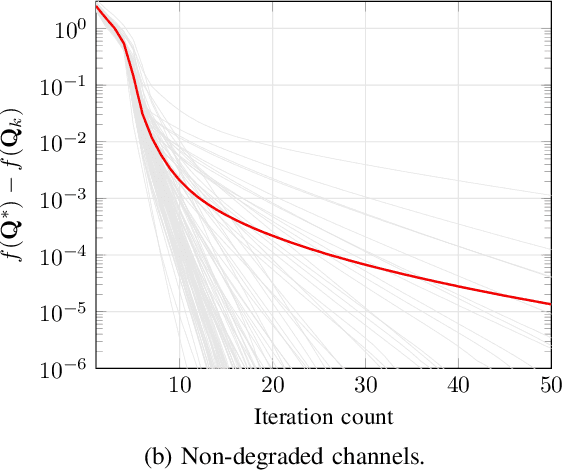
To achieve perfect secrecy in a multiple-input multiple-output (MIMO) Gaussian wiretap channel (WTC), we need to find its secrecy capacity and optimal signaling, which involves solving a difference of convex functions program known to be non-convex for the non-degraded case. To deal with this, a class of existing solutions have been developed but only local optimality is guaranteed by standard convergence analysis. Interestingly, our extensive numerical experiments have shown that these local optimization methods indeed achieve global optimality. In this paper, we provide an analytical proof for this observation. To achieve this, we show that the Karush-Kuhn-Tucker (KKT) conditions of the secrecy rate maximization problem admit a unique solution for both degraded and non-degraded cases. Motivated by this, we also propose a low-complexity algorithm to find a stationary point. Numerical results are presented to verify the theoretical analysis.

Efficient Numerical Methods for Secrecy Capacity of Gaussian MIMO Wiretap Channel

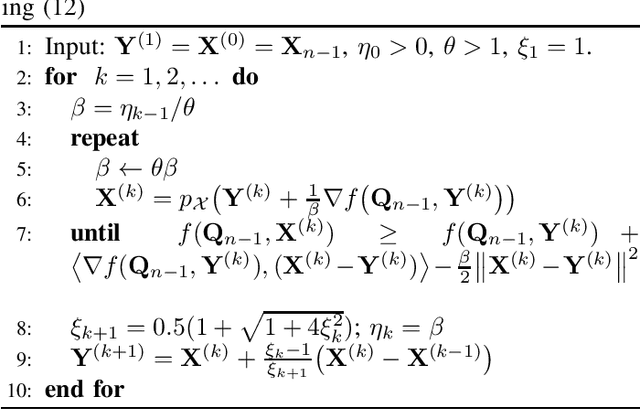
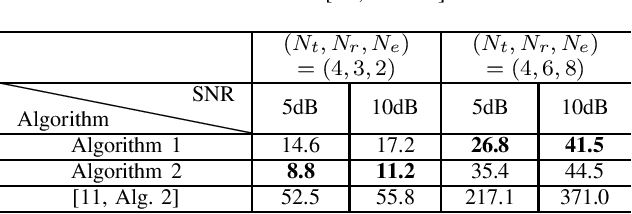
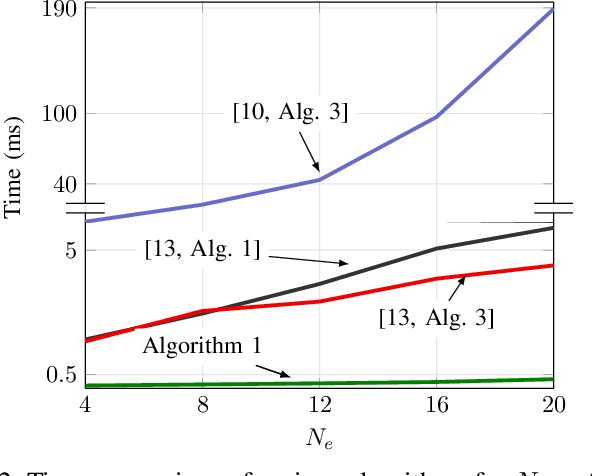
This paper presents two different low-complexity methods for obtaining the secrecy capacity of multiple-input multiple-output (MIMO) wiretap channel subject to a sum power constraint (SPC). The challenges in deriving computationally efficient solutions to the secrecy capacity problem are due to the fact that the secrecy rate is a difference of convex functions (DC) of the transmit covariance matrix, for which its convexity is only known for \emph{the degraded case}. In the first method, we capitalize on the accelerated DC algorithm, which requires solving a sequence of convex subproblems. In particular, we show that each subproblem indeed admits a water-filling solution. In the second method, based on the equivalent convex-concave reformulation of the secrecy capacity problem, we develop a so-called partial best response algorithm (PBRA). Each iteration of the PBRA is also done in closed form. Simulation results are provided to demonstrate the superior performance of the proposed methods.