Probabilistic Pixel-Adaptive Refinement Networks

Encoder-decoder networks have found widespread use in various dense prediction tasks. However, the strong reduction of spatial resolution in the encoder leads to a loss of location information as well as boundary artifacts. To address this, image-adaptive post-processing methods have shown beneficial by leveraging the high-resolution input image(s) as guidance data. We extend such approaches by considering an important orthogonal source of information: the network's confidence in its own predictions. We introduce probabilistic pixel-adaptive convolutions (PPACs), which not only depend on image guidance data for filtering, but also respect the reliability of per-pixel predictions. As such, PPACs allow for image-adaptive smoothing and simultaneously propagating pixels of high confidence into less reliable regions, while respecting object boundaries. We demonstrate their utility in refinement networks for optical flow and semantic segmentation, where PPACs lead to a clear reduction in boundary artifacts. Moreover, our proposed refinement step is able to substantially improve the accuracy on various widely used benchmarks.

Learning Task-Specific Generalized Convolutions in the Permutohedral Lattice

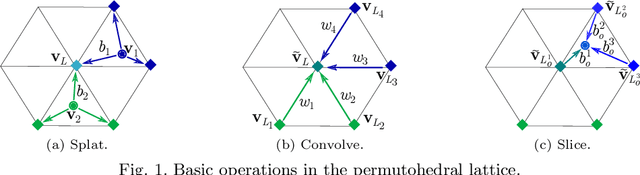
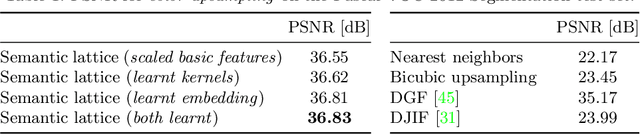
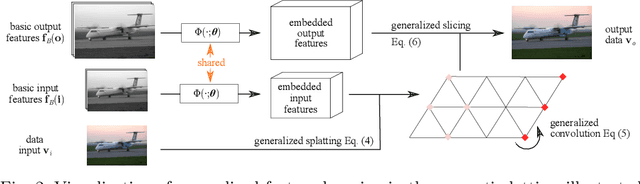
Dense prediction tasks typically employ encoder-decoder architectures, but the prevalent convolutions in the decoder are not image-adaptive and can lead to boundary artifacts. Different generalized convolution operations have been introduced to counteract this. We go beyond these by leveraging guidance data to redefine their inherent notion of proximity. Our proposed network layer builds on the permutohedral lattice, which performs sparse convolutions in a high-dimensional space allowing for powerful non-local operations despite small filters. Multiple features with different characteristics span this permutohedral space. In contrast to prior work, we learn these features in a task-specific manner by generalizing the basic permutohedral operations to learnt feature representations. As the resulting objective is complex, a carefully designed framework and learning procedure are introduced, yielding rich feature embeddings in practice. We demonstrate the general applicability of our approach in different joint upsampling tasks. When adding our network layer to state-of-the-art networks for optical flow and semantic segmentation, boundary artifacts are removed and the accuracy is improved.

Stochastic Variational Inference with Gradient Linearization

Variational inference has experienced a recent surge in popularity owing to stochastic approaches, which have yielded practical tools for a wide range of model classes. A key benefit is that stochastic variational inference obviates the tedious process of deriving analytical expressions for closed-form variable updates. Instead, one simply needs to derive the gradient of the log-posterior, which is often much easier. Yet for certain model classes, the log-posterior itself is difficult to optimize using standard gradient techniques. One such example are random field models, where optimization based on gradient linearization has proven popular, since it speeds up convergence significantly and can avoid poor local optima. In this paper we propose stochastic variational inference with gradient linearization (SVIGL). It is similarly convenient as standard stochastic variational inference - all that is required is a local linearization of the energy gradient. Its benefit over stochastic variational inference with conventional gradient methods is a clear improvement in convergence speed, while yielding comparable or even better variational approximations in terms of KL divergence. We demonstrate the benefits of SVIGL in three applications: Optical flow estimation, Poisson-Gaussian denoising, and 3D surface reconstruction.

ProbFlow: Joint Optical Flow and Uncertainty Estimation

Optical flow estimation remains challenging due to untextured areas, motion boundaries, occlusions, and more. Thus, the estimated flow is not equally reliable across the image. To that end, post-hoc confidence measures have been introduced to assess the per-pixel reliability of the flow. We overcome the artificial separation of optical flow and confidence estimation by introducing a method that jointly predicts optical flow and its underlying uncertainty. Starting from common energy-based formulations, we rely on the corresponding posterior distribution of the flow given the images. We derive a variational inference scheme based on mean field, which incorporates best practices from energy minimization. An uncertainty measure is obtained along the flow at every pixel as the (marginal) entropy of the variational distribution. We demonstrate the flexibility of our probabilistic approach by applying it to two different energies and on two benchmarks. We not only obtain flow results that are competitive with the underlying energy minimization approach, but also a reliable uncertainty measure that significantly outperforms existing post-hoc approaches.