GrINd: Grid Interpolation Network for Scattered Observations

Predicting the evolution of spatiotemporal physical systems from sparse and scattered observational data poses a significant challenge in various scientific domains. Traditional methods rely on dense grid-structured data, limiting their applicability in scenarios with sparse observations. To address this challenge, we introduce GrINd (Grid Interpolation Network for Scattered Observations), a novel network architecture that leverages the high-performance of grid-based models by mapping scattered observations onto a high-resolution grid using a Fourier Interpolation Layer. In the high-resolution space, a NeuralPDE-class model predicts the system's state at future timepoints using differentiable ODE solvers and fully convolutional neural networks parametrizing the system's dynamics. We empirically evaluate GrINd on the DynaBench benchmark dataset, comprising six different physical systems observed at scattered locations, demonstrating its state-of-the-art performance compared to existing models. GrINd offers a promising approach for forecasting physical systems from sparse, scattered observational data, extending the applicability of deep learning methods to real-world scenarios with limited data availability.

TaylorPDENet: Learning PDEs from non-grid Data

Modeling data obtained from dynamical systems has gained attention in recent years as a challenging task for machine learning models. Previous approaches assume the measurements to be distributed on a grid. However, for real-world applications like weather prediction, the observations are taken from arbitrary locations within the spatial domain. In this paper, we propose TaylorPDENet - a novel machine learning method that is designed to overcome this challenge. Our algorithm uses the multidimensional Taylor expansion of a dynamical system at each observation point to estimate the spatial derivatives to perform predictions. TaylorPDENet is able to accomplish two objectives simultaneously: accurately forecast the evolution of a complex dynamical system and explicitly reconstruct the underlying differential equation describing the system. We evaluate our model on a variety of advection-diffusion equations with different parameters and show that it performs similarly to equivalent approaches on grid-structured data while being able to process unstructured data as well.

DynaBench: A benchmark dataset for learning dynamical systems from low-resolution data

Previous work on learning physical systems from data has focused on high-resolution grid-structured measurements. However, real-world knowledge of such systems (e.g. weather data) relies on sparsely scattered measuring stations. In this paper, we introduce a novel simulated benchmark dataset, DynaBench, for learning dynamical systems directly from sparsely scattered data without prior knowledge of the equations. The dataset focuses on predicting the evolution of a dynamical system from low-resolution, unstructured measurements. We simulate six different partial differential equations covering a variety of physical systems commonly used in the literature and evaluate several machine learning models, including traditional graph neural networks and point cloud processing models, with the task of predicting the evolution of the system. The proposed benchmark dataset is expected to advance the state of art as an out-of-the-box easy-to-use tool for evaluating models in a setting where only unstructured low-resolution observations are available. The benchmark is available at https://anonymous.4open.science/r/code-2022-dynabench/.

Do Different Deep Metric Learning Losses Lead to Similar Learned Features?

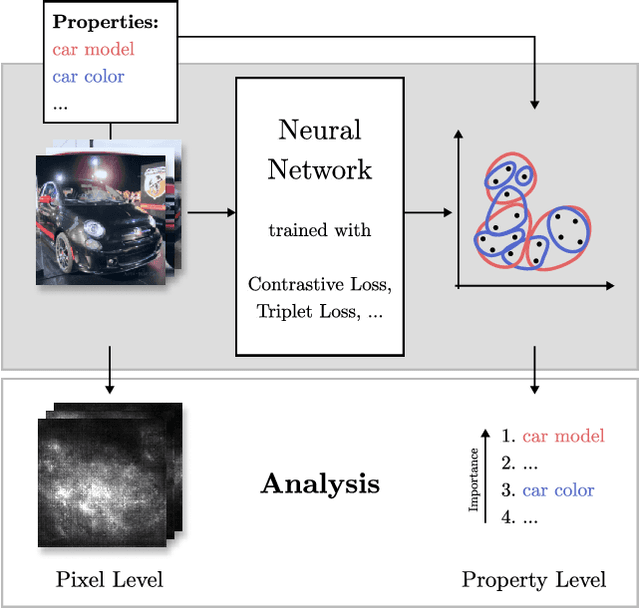
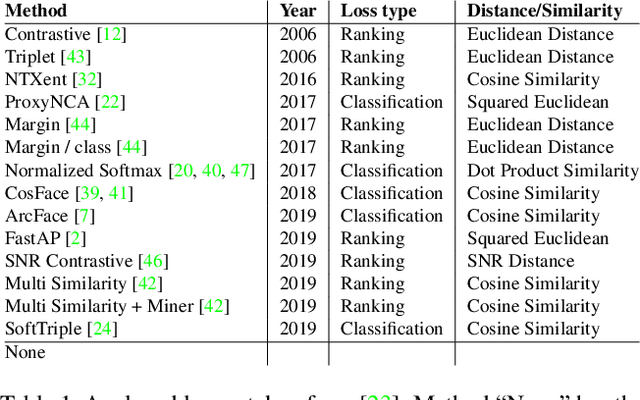
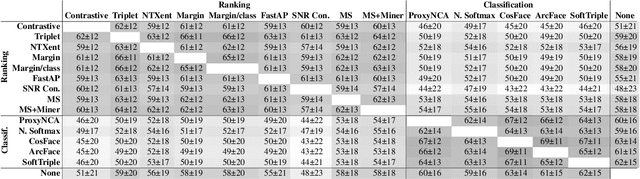
Recent studies have shown that many deep metric learning loss functions perform very similarly under the same experimental conditions. One potential reason for this unexpected result is that all losses let the network focus on similar image regions or properties. In this paper, we investigate this by conducting a two-step analysis to extract and compare the learned visual features of the same model architecture trained with different loss functions: First, we compare the learned features on the pixel level by correlating saliency maps of the same input images. Second, we compare the clustering of embeddings for several image properties, e.g. object color or illumination. To provide independent control over these properties, photo-realistic 3D car renders similar to images in the Cars196 dataset are generated. In our analysis, we compare 14 pretrained models from a recent study and find that, even though all models perform similarly, different loss functions can guide the model to learn different features. We especially find differences between classification and ranking based losses. Our analysis also shows that some seemingly irrelevant properties can have significant influence on the resulting embedding. We encourage researchers from the deep metric learning community to use our methods to get insights into the features learned by their proposed methods.

NeuralPDE: Modelling Dynamical Systems from Data

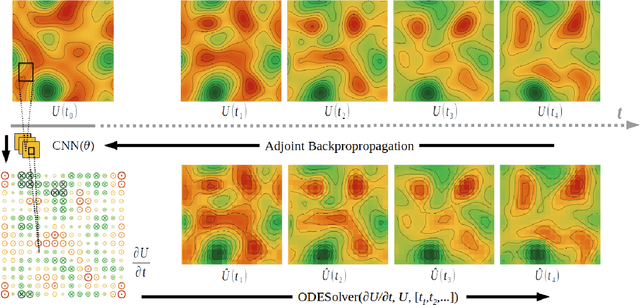
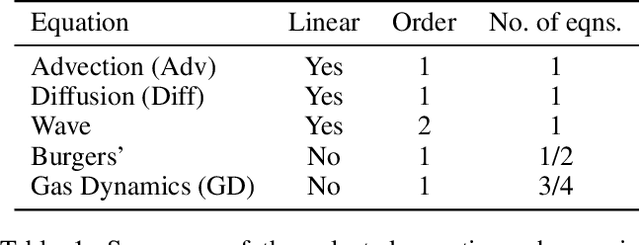
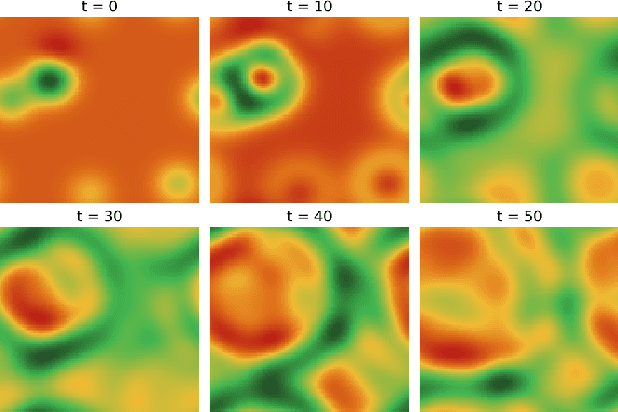
Many physical processes such as weather phenomena or fluid mechanics are governed by partial differential equations (PDEs). Modelling such dynamical systems using Neural Networks is an emerging research field. However, current methods are restricted in various ways: they require prior knowledge about the governing equations, and are limited to linear or first-order equations. In this work we propose NeuralPDE, a model which combines convolutional neural networks (CNNs) with differentiable ODE solvers to model dynamical systems. We show that the Method of Lines used in standard PDE solvers can be represented using convolutions which makes CNNs the natural choice to parametrize arbitrary PDE dynamics. Our model can be applied to any data without requiring any prior knowledge about the governing PDE. We evaluate NeuralPDE on datasets generated by solving a wide variety of PDEs, covering higher orders, non-linear equations and multiple spatial dimensions.