NeuralPDE: Modelling Dynamical Systems from Data
Paper and Code
Nov 15, 2021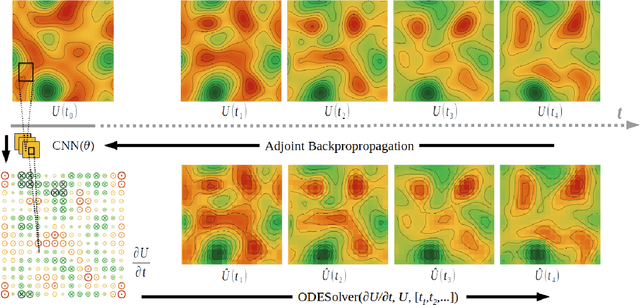
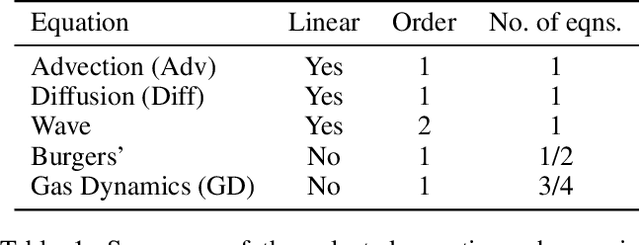

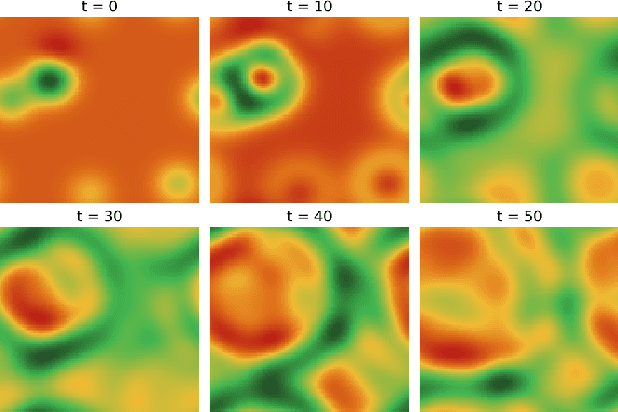
Many physical processes such as weather phenomena or fluid mechanics are governed by partial differential equations (PDEs). Modelling such dynamical systems using Neural Networks is an emerging research field. However, current methods are restricted in various ways: they require prior knowledge about the governing equations, and are limited to linear or first-order equations. In this work we propose NeuralPDE, a model which combines convolutional neural networks (CNNs) with differentiable ODE solvers to model dynamical systems. We show that the Method of Lines used in standard PDE solvers can be represented using convolutions which makes CNNs the natural choice to parametrize arbitrary PDE dynamics. Our model can be applied to any data without requiring any prior knowledge about the governing PDE. We evaluate NeuralPDE on datasets generated by solving a wide variety of PDEs, covering higher orders, non-linear equations and multiple spatial dimensions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge