PIVOTS: Aligning unseen Structures using Preoperative to Intraoperative Volume-To-Surface Registration for Liver Navigation

Non-rigid registration is essential for Augmented Reality guided laparoscopic liver surgery by fusing preoperative information, such as tumor location and vascular structures, into the limited intraoperative view, thereby enhancing surgical navigation. A prerequisite is the accurate prediction of intraoperative liver deformation which remains highly challenging due to factors such as large deformation caused by pneumoperitoneum, respiration and tool interaction as well as noisy intraoperative data, and limited field of view due to occlusion and constrained camera movement. To address these challenges, we introduce PIVOTS, a Preoperative to Intraoperative VOlume-To-Surface registration neural network that directly takes point clouds as input for deformation prediction. The geometric feature extraction encoder allows multi-resolution feature extraction, and the decoder, comprising novel deformation aware cross attention modules, enables pre- and intraoperative information interaction and accurate multi-level displacement prediction. We train the neural network on synthetic data simulated from a biomechanical simulation pipeline and validate its performance on both synthetic and real datasets. Results demonstrate superior registration performance of our method compared to baseline methods, exhibiting strong robustness against high amounts of noise, large deformation, and various levels of intraoperative visibility. We publish the training and test sets as evaluation benchmarks and call for a fair comparison of liver registration methods with volume-to-surface data. Code and datasets are available here https://github.com/pengliu-nct/PIVOTS.

clDice -- a Topology-Preserving Loss Function for Tubular Structure Segmentation

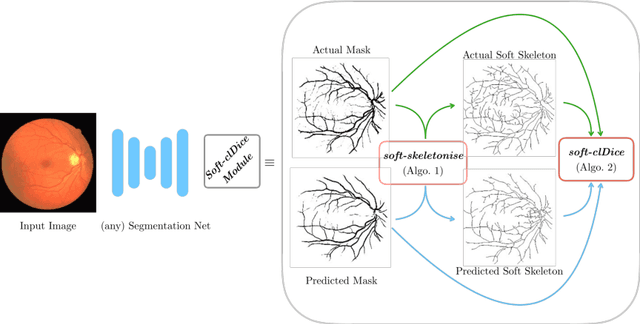
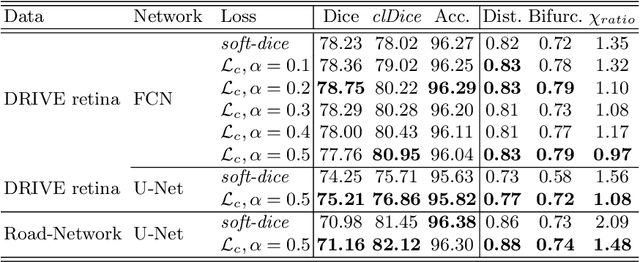
Accurate segmentation of tubular, network-like structures, such as vessels, neurons, or roads, is relevant to many fields of research. For such structures, the topology is their most important characteristic, e.g. preserving connectedness: in case of vascular networks, missing a connected vessel entirely alters the blood-flow dynamics. We introduce a novel similarity measure termed clDice, which is calculated on the intersection of the segmentation masks and their (morphological) skeletons. Crucially, we theoretically prove that clDice guarantees topological correctness for binary 2D and 3D segmentation. Extending this, we propose a computationally efficient, differentiable soft-clDice as a loss function for training arbitrary neural segmentation networks. We benchmark the soft-clDice loss for segmentation on four public datasets (2D and 3D). Training on soft-clDice leads to segmentation with more accurate connectivity information, higher graph similarity, and better volumetric scores.