Algorithm Configuration: Learning policies for the quick termination of poor performers

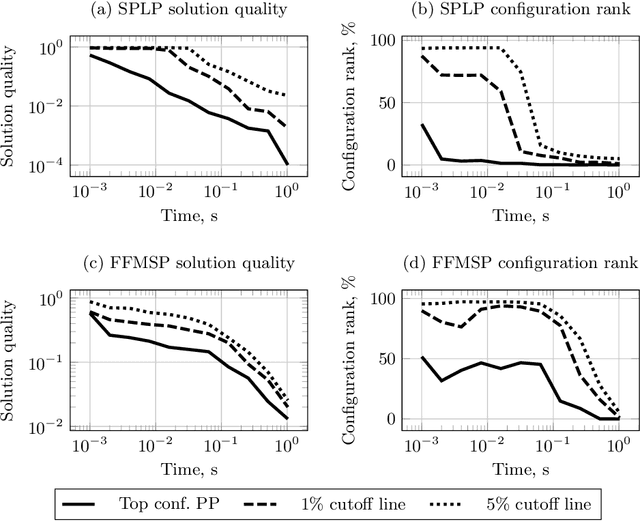
One way to speed up the algorithm configuration task is to use short runs instead of long runs as much as possible, but without discarding the configurations that eventually do well on the long runs. We consider the problem of selecting the top performing configurations of the Conditional Markov Chain Search (CMCS), a general algorithm schema that includes, for examples, VNS. We investigate how the structure of performance on short tests links with those on long tests, showing that significant differences arise between test domains. We propose a "performance envelope" method to exploit the links; that learns when runs should be terminated, but that automatically adapts to the domain.

Pattern-Based Approach to the Workflow Satisfiability Problem with User-Independent Constraints

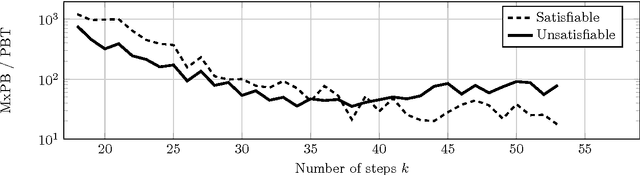
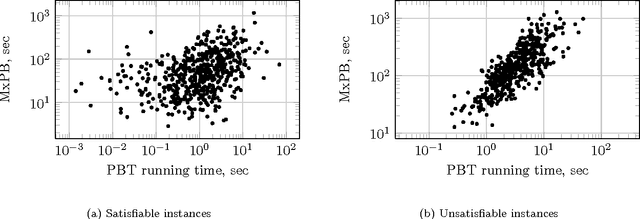
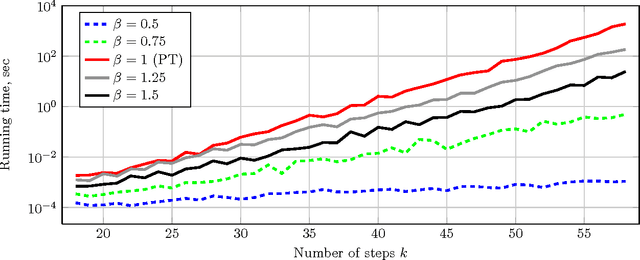
The fixed parameter tractable (FPT) approach is a powerful tool in tackling computationally hard problems. In this paper, we link FPT results to classic artificial intelligence (AI) techniques to show how they complement each other. Specifically, we consider the workflow satisfiability problem (WSP) which asks whether there exists an assignment of authorised users to the steps in a workflow specification, subject to certain constraints on the assignment. It was shown by Cohen et al. (JAIR 2014) that WSP restricted to the class of user-independent constraints (UI), covering many practical cases, admits FPT algorithms, i.e. can be solved in time exponential only in the number of steps $k$ and polynomial in the number of users $n$. Since usually $k \ll n$ in WSP, such FPT algorithms are of great practical interest as they significantly extend the size of the problem that can be routinely solved. We give a new view of the FPT nature of the WSP with UI constraints, showing that it decomposes the problem into two levels. Exploiting this two-level split, we develop a new FPT algorithm that is by many orders of magnitude faster than the previous state-of-the-art WSP algorithm; and it also has only polynomial space complexity whereas the old algorithm takes memory exponential in $k$, which limits its application. We also provide a new pseudo-boolean (PB) formulation of the WSP with UI constraints which exploits this new decomposition of the problem into two levels. Our experiments show that efficiency of solving this new PB formulation of the problem by a general purpose PB solver can be close to the bespoke FPT algorithm, which raises the potential of using general purpose solvers to tackle FPT problems efficiently. We also study the computational performance of various algorithms to complement the overly-pessimistic worst-case analysis that is usually done in FPT studies.

Markov Chain methods for the bipartite Boolean quadratic programming problem

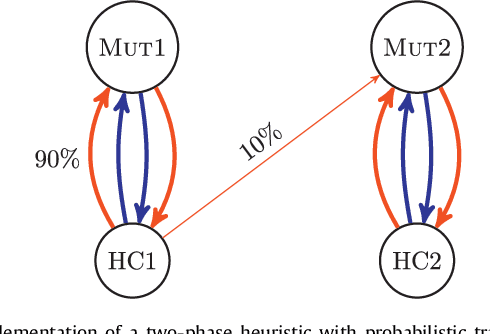
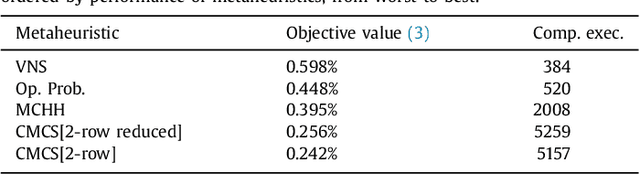
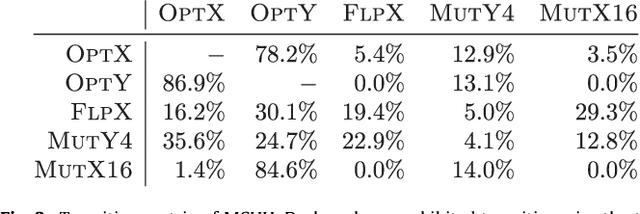
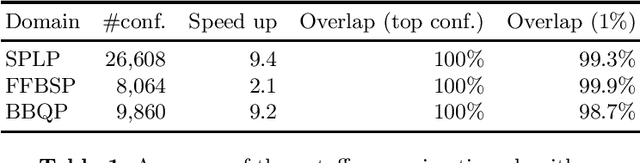
We study the Bipartite Boolean Quadratic Programming Problem (BBQP) which is an extension of the well known Boolean Quadratic Programming Problem (BQP). Applications of the BBQP include mining discrete patterns from binary data, approximating matrices by rank-one binary matrices, computing the cut-norm of a matrix, and solving optimisation problems such as maximum weight biclique, bipartite maximum weight cut, maximum weight induced sub-graph of a bipartite graph, etc. For the BBQP, we first present several algorithmic components, specifically, hill climbers and mutations, and then show how to combine them in a high-performance metaheuristic. Instead of hand-tuning a standard metaheuristic to test the efficiency of the hybrid of the components, we chose to use an automated generation of a multi-component metaheuristic to save human time, and also improve objectivity in the analysis and comparisons of components. For this we designed a new metaheuristic schema which we call Conditional Markov Chain Search (CMCS). We show that CMCS is flexible enough to model several standard metaheuristics; this flexibility is controlled by multiple numeric parameters, and so is convenient for automated generation. We study the configurations revealed by our approach and show that the best of them outperforms the previous state-of-the-art BBQP algorithm by several orders of magnitude. In our experiments we use benchmark instances introduced in the preliminary version of this paper and described here, which have already become the de facto standard in the BBQP literature.

Combining Monte-Carlo and Hyper-heuristic methods for the Multi-mode Resource-constrained Multi-project Scheduling Problem

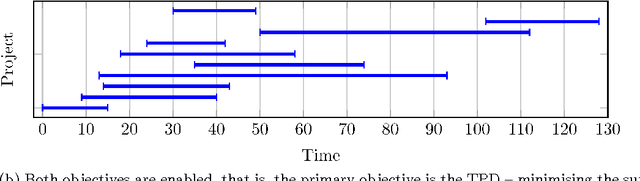
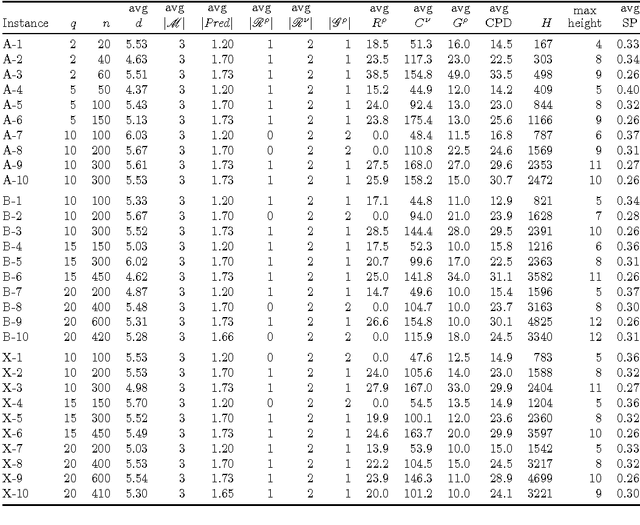
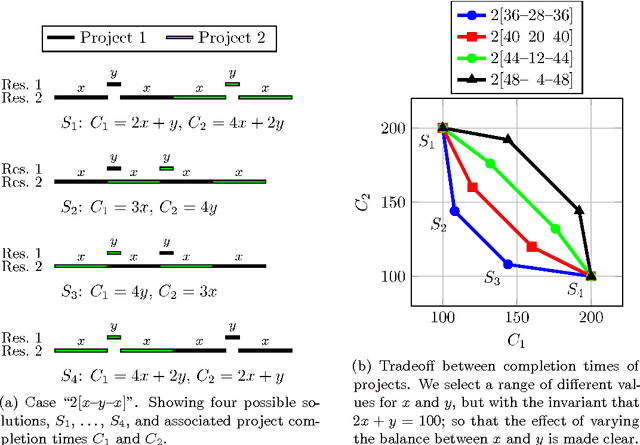
Multi-mode resource and precedence-constrained project scheduling is a well-known challenging real-world optimisation problem. An important variant of the problem requires scheduling of activities for multiple projects considering availability of local and global resources while respecting a range of constraints. A critical aspect of the benchmarks addressed in this paper is that the primary objective is to minimise the sum of the project completion times, with the usual makespan minimisation as a secondary objective. We observe that this leads to an expected different overall structure of good solutions and discuss the effects this has on the algorithm design. This paper presents a carefully designed hybrid of Monte-Carlo tree search, novel neighbourhood moves, memetic algorithms, and hyper-heuristic methods. The implementation is also engineered to increase the speed with which iterations are performed, and to exploit the computing power of multicore machines. Empirical evaluation shows that the resulting information-sharing multi-component algorithm significantly outperforms other solvers on a set of "hidden" instances, i.e. instances not available at the algorithm design phase.

Decomposition, Reformulation, and Diving in University Course Timetabling

In many real-life optimisation problems, there are multiple interacting components in a solution. For example, different components might specify assignments to different kinds of resource. Often, each component is associated with different sets of soft constraints, and so with different measures of soft constraint violation. The goal is then to minimise a linear combination of such measures. This paper studies an approach to such problems, which can be thought of as multiphase exploitation of multiple objective-/value-restricted submodels. In this approach, only one computationally difficult component of a problem and the associated subset of objectives is considered at first. This produces partial solutions, which define interesting neighbourhoods in the search space of the complete problem. Often, it is possible to pick the initial component so that variable aggregation can be performed at the first stage, and the neighbourhoods to be explored next are guaranteed to contain feasible solutions. Using integer programming, it is then easy to implement heuristics producing solutions with bounds on their quality. Our study is performed on a university course timetabling problem used in the 2007 International Timetabling Competition, also known as the Udine Course Timetabling Problem. In the proposed heuristic, an objective-restricted neighbourhood generator produces assignments of periods to events, with decreasing numbers of violations of two period-related soft constraints. Those are relaxed into assignments of events to days, which define neighbourhoods that are easier to search with respect to all four soft constraints. Integer programming formulations for all subproblems are given and evaluated using ILOG CPLEX 11. The wider applicability of this approach is analysed and discussed.